练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数是的导函数.

    （Ⅰ）当时，对于任意的，求的最小值；

    （Ⅱ）若存在，使，求的取值范围.

    【答案】（1）最小值为-11.（2）

    【解析】试题分析：(1)欲求的最小值,就分别求的最小值
    (2)存在,使即寻找是变量的范围.

    试题解析：

    解：（Ⅰ）由题意得.

    令，得或.

    当在[-1,1]上变化时，，随的变化情况如下表：

    -1

    (-1,0)

    0

    （0,1）

    1

    -7

    -

    0

    1

    -1

    -4

    -3

    ∴对于，的最小值为.

    ∵的对称轴为直线，且抛物线开口向下，

    ∴对于，的最小值为.

    ∴的最小值为-11.

    （Ⅱ）∵.

    ①若，当时，.

    ∴在上单调递减.

    又，则当时，.

    ∴当时，不存在，使.

    ②若，则当时，；当时，.

    从而在上单调递增，在上单调递减.

    ∴当时，.

    根据题意，得，即，解得.

    综上，的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某工厂生产某种水杯，每个水杯的原材料费、加工费分别为30元、m元(m为常数，且2≤m≤3)，设每个水杯的出厂价为x元(35≤x≤41)，根据市场调查，水杯的日销售量与ex(e为自然对数的底数)成反比例，已知每个水杯的出厂价为40元时，日销售量为10个．

    (1)求该工厂的日利润y(元)与每个水杯的出厂价x(元)的函数关系式；

    (2)当每个水杯的出厂价为多少元时，该工厂的日利润最大，并求日利润的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】电视台播放甲、乙两套连续剧，每次播放连续剧时，需要播放广告．已知每次播放甲、乙两套连续剧时，连续剧播放时长、广告播放时长、收视人次如下表所示：

    连续剧播放时长（分钟）

    广告播放时长（分钟）

    收视人次（万）

    甲

    70

    5

    60

    乙

    60

    5

    25

    已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟，广告的总播放时间不少于30分钟，且甲连续剧播放的次数不多于乙连续剧播放次数的2倍．分别用，表示每周计划播出的甲、乙两套连续剧的次数．

    （1）用，列出满足题目条件的数学关系式，并画出相应的平面区域；

    （2）问电视台每周播出甲、乙两套连续剧各多少次，才能使收视人次最多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面内三个向量： =（3，2）， =（﹣1，2）， =（4，1）
    （1）若（ +k ）∥（2 ﹣ ），求实数k的值；
    （2）设 =（x，y），且满足（ + ）⊥（ ﹣ ），| ﹣ |= ，求 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2＝4x的焦点为F，过点F的直线l与C相交于A，B两点，若|AB|＝8，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：不等式(m－1)x2＋(m－1)x＋2>0的解集是R，命题q：sin x＋cos x>m.如果对于任意的x∈R，命题p是真命题且命题q为假命题，求m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

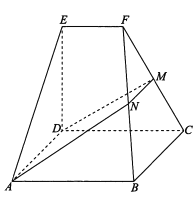
    【题目】如图，在几何体中，底面为矩形， ， ， ， ， 为棱上一点，平面与棱交于点.

    （Ⅰ）求证： ；

    （Ⅱ）求证： ；

    （Ⅲ）若，试问平面是否可能与平面垂直？若能，求出值；若不能，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】以直角坐标系的原点为极点， 轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线的参数方程为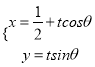，（ 为参数， ），曲线的极坐标方程为.

    （1）求曲线的直角坐标方程；

    （2）设直线与曲线相交于， 两点，当变化时，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆关于直线对称的圆为.

    （1）求圆的方程；

    （2）过点作直线与圆交于两点， 是坐标原点，是否存在这样的直线，使得在平行四边形中？若存在，求出所有满足条件的直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案