
【题目】已知![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() 对于任意的
对于任意的![]() 成立.
成立.
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减;当
内单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,在
内单调递减,在![]() 内单调递增;当
内单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增;当
内单调递增;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,在
内单调递减,在![]() 内单调递增;(2)详见解析.
内单调递增;(2)详见解析.
【解析】
试题分析:(1)首先求出函数的定义域,然后求出其导函数,并对a进行分类讨论:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结合导数大于0和小于0所对应的自变量的取值范围,进而得出所求的结论;(2)构造函数
,结合导数大于0和小于0所对应的自变量的取值范围,进而得出所求的结论;(2)构造函数![]() ,则
,则![]() ,然后分别求出
,然后分别求出![]() ,
,![]() ,利用导数研究函数的单调性与最值即可得出函数
,利用导数研究函数的单调性与最值即可得出函数![]() 的最小值,最后结合已知得出所求的结果即可.
的最小值,最后结合已知得出所求的结果即可.
试题解析:(1)解:![]() 的定义域为
的定义域为![]() ,
,![]() 当
当![]() ,
,![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() ,
,![]() 单调递减.当
单调递减.当![]() 时,
时,![]() .①
.①![]() 时
时![]() ,当
,当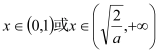 时,
时,![]() 单调递增,当
单调递增,当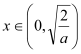 时,
时,![]() 单调递减;②
单调递减;②![]() 时
时![]() ,当
,当![]() 时
时![]() 单调递增;③
单调递增;③![]() 时,
时,![]() ,当
,当 单调递增,当
单调递增,当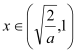 时,
时,![]() 单调递减.
单调递减.
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减;
内单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,在
内单调递减,在![]() 内单调递增;
内单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
(2)由(1)知,![]() 时,
时,
![]()
![]() ,设
,设![]()
![]() 则
则
由![]() 可得
可得![]() ,当且仅当x=1时取等号
,当且仅当x=1时取等号
又![]() ,设
,设![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,
![]()
![]() 使得
使得![]() ,
,
![]() 在
在![]() ,上单调递增,在
,上单调递增,在![]() 上单调递减
上单调递减
![]() 当且仅当
当且仅当![]() 时等号成立,
时等号成立,![]() ,即
,即![]() 对于任意的
对于任意的![]() 成立.
成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,
则P(-2≤ξ≤2)=( )
A. 0.477 B. 0.628 C. 0.954 D. 0.977
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数: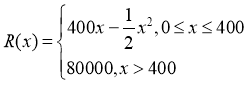 ,其中
,其中![]() 是仪器的月产量.
是仪器的月产量.
(1) 将利润表示为月产量的函数![]() ;
;
(2) 当月产量为何值时,公司所获利润最大?最大利润为多少元? (利润=总收益-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形.已知
是等边三角形.已知![]() ,
,![]() ,
,![]() .
.

(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 点位于线段
点位于线段![]() 什么位置时,
什么位置时,![]() 平面
平面![]() ?
?
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,以椭圆短轴为直径的圆经过点
,以椭圆短轴为直径的圆经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() 的斜率分别为
的斜率分别为![]() ,问
,问![]() 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点.
的中点.

(1)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置并证明结论;若不存在,请说明理由.
的位置并证明结论;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2-3,值域为{1,5}的“孪生函数”共有( )
A.10个
B.9个
C.8个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com