练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    （1）求曲线在点处的切线方程；

    （2）若函数有两个极值点，，且不等式恒成立，求实数的取值范围.

    【答案】（1）（2）

    【解析】

    （1）对进行求导，得，利用导数的几何意义求出切线斜率，最后根据点斜式求出切线方程；

    （2）根据题意，化简得，求出导函数，通过有两个不同的正根，即有两个不同的正根，列出不等式组，由恒成立条件转化为恒成立，构造新函数，利用导函数研究函数单调性和最值，进而可求得的取值范围.

    解：（1）因为，

    所以，

    所以切线斜率，又，

    故曲线在点处的切线方程为：

    ，即.

    （2）因为，

    所以，

    因为函数有两个极值点，，

    则有两个不同的正根，即有两个不同的正根，

    则，

    不等式恒成立等价于

    恒成立，

    又

    ，

    所以，

    令，则，

    所以在上单调递减，

    所以，所以.

    所以实数的取值范围为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

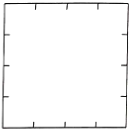
    【题目】已知一块边长为4的正方形铝板（如图），请设计一种裁剪方法，用虚线标示在答题卡本题图中，通过该方案裁剪，可焊接做成一个密封的正四棱柱（底面是正方形且侧棱垂于底面的四棱柱），且该四棱柱的全面积等于正方形铝板的面积（要求裁剪的块数尽可能少，不计焊接缝的面积），则该四棱柱外接球的体积为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】受疫情影响，某电器厂生产的空调滞销，经研究决定，在已有线下门店销售的基础上，成立线上营销团队，大力发展“网红”经济，当线下销售人数为（人）时，每天线下销售空调可达（百台），当线上销售人数为（人）（）时，每天线上销量达到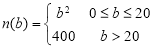（百台）.

    （1）解不等式：，并解释其实际意义；

    （2）若该工厂大有销售人员（）人，按市场需求，安排人员进行线上或线下销售，问该工厂每天销售空调总台数的最大值是多少百台？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知曲线的参数方程为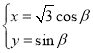：，（为参数），以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为

    （1）求曲线和直线l的直角坐标方程；

    （2）若点在曲线上，且点到直线l的距离最小，求点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若函数在区间上单调递减，求实数a的取值范围；

    （2）当，（）时，求证：；

    （3）若函数有两个极值点，，求证：（e为自然对数的底数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项数列，满足：对任意正整数，都有，，成等差数列，，，成等比数列，且，．

    （Ⅰ）求证：数列是等差数列；

    （Ⅱ）求数列，的通项公式；

    （Ⅲ）设=++…+，如果对任意的正整数，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中， ，动点满足：以为直径的圆与轴相切.

    （1）求点的轨迹方程；

    （2）设点的轨迹为曲线，直线过点且与交于两点，当与的面积之和取得最小值时，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    求不等式的解集；

    若函数的最小值为，整数、满足，求证.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线是平面和平面的交线，异面直线，分别在平面和平面内.

    命题：直线，中至多有一条与直线相交；

    命题：直线，中至少有一条与直线相交；

    命题：直线，都不与直线相交.

    则下列命题中是真命题的为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案