
 x2与g(x)=elnx,是否存在公共切线y=kx+b(常数k,b)使得h(x)≥kx+b和g(x)≤kx+b在函数h(x),g(x)各自定义域上恒成立?若存在,求出该直线的方程;若不存在,请说明理由.
x2与g(x)=elnx,是否存在公共切线y=kx+b(常数k,b)使得h(x)≥kx+b和g(x)≤kx+b在函数h(x),g(x)各自定义域上恒成立?若存在,求出该直线的方程;若不存在,请说明理由.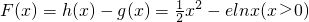 ,∴
,∴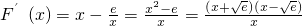
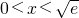 时,F′(x)<0,函数F(x)单调递减;当
时,F′(x)<0,函数F(x)单调递减;当 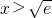 时,F′(x)>0,函数F(x)单调递增.
时,F′(x)>0,函数F(x)单调递增. 是函数F(x)的极小值点,也是最小值点,∴
是函数F(x)的极小值点,也是最小值点,∴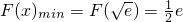 ,∴函数f(x)与h(x)的图象在
,∴函数f(x)与h(x)的图象在  处有公共点
处有公共点 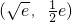 (9分)
(9分)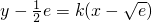 ,令函数
,令函数 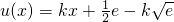 ,
,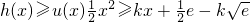 在x∈R恒成立,即
在x∈R恒成立,即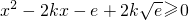 在R上恒成立,
在R上恒成立,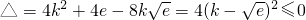 成立,
成立,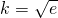 ,故
,故 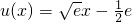 .(11分)
.(11分)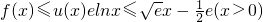 恒成立
恒成立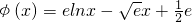 ,则
,则 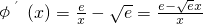 .
.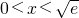 时,φ′(x)>0,函数φ(x)单调递增;当
时,φ′(x)>0,函数φ(x)单调递增;当 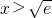 时,φ′(x)<0.函数φ(x)单调递减.∴
时,φ′(x)<0.函数φ(x)单调递减.∴ 时φ(x)取得最大值0,则
时φ(x)取得最大值0,则  (x>0)成立.(13分)
(x>0)成立.(13分)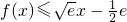 且
且 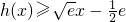 ,
,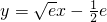 ,此时
,此时 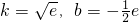 .(14分)
.(14分)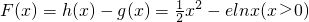 ,原问题转化为研究此函数的单调性问题,利用导数知识解决.
,原问题转化为研究此函数的单调性问题,利用导数知识解决.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com