
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() ,利用导数讨论函数的单调性,求出最小值,即可得到实数
,利用导数讨论函数的单调性,求出最小值,即可得到实数![]() 的值;(2)由(1)知
的值;(2)由(1)知![]() ,即
,即![]() ,
,
令![]() (
(![]() ,
, ![]() )则
)则![]() ,所以
,所以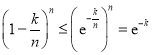 ,令
,令![]() ,求和后利用放缩法可得
,求和后利用放缩法可得![]() ,从而可得
,从而可得![]() 的最小值.
的最小值.
所以 ,.
,.
试题解析:(1)因为![]()
所以![]() ,
,
由![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() ,
,
由![]() ,
,
(i)当![]() 时,
时, ![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
所以![]() 时,
时, ![]() ,
,
所以不满足题意.
(ii)当![]() 时,由
时,由![]() ,得
,得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]() .
.
设![]() ,所以
,所以![]() ,①
,①
因为![]()
令![]() 得
得![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() ,②
,②
由①②得![]() ,则
,则![]() .
.
(2)由(1)知![]() ,即
,即![]() ,
,
令![]() (
(![]() ,
, ![]() )则
)则![]() ,
,
所以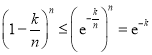 ,
,
所以![]()
![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某班有24名男生和26名女生,数据a1 , a2 , …,a50是该班50名学生在一次数学学业水平模拟考试的成绩,下面的程序用来同时统计全班成绩的平均数:A,男生平均分:M,女生平均分:W;为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其成绩的相反数,那么在图里空白的判断框和处理框中,应分别填入下列四个选项中的( ) 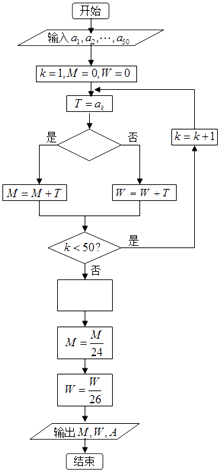
A.T>0?, ![]()
B.T<0?, ![]() ??
??
C.T<0?, ![]()
D.T>0?, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1CC1 . 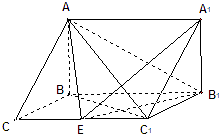
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1(要求说明理由).
(3)在(2)的条件下,若AB= ![]() ,求二面角A﹣EB1﹣A1的大小.
,求二面角A﹣EB1﹣A1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() 是不共线的四点,则
是不共线的四点,则![]() 是四边形
是四边形![]() 为平行四边形的充要条件;
为平行四边形的充要条件;
③若![]() ,
, ![]() ,则
,则![]() ;
;
④![]() 的充要条件是
的充要条件是![]() 且
且![]()
其中正确命题的序号是( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com