
【题目】如图,在四边形![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() ,
, ![]() ,
,
![]() ,
, ![]() 的面积为
的面积为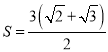 ,
, ![]() 为锐角.
为锐角.

(Ⅰ)求![]() ;
;
(Ⅱ)求![]() .
.
【答案】(I) ![]() . (II)
. (II) ![]() .
.
【解析】试题分析: (I)在![]() 中,由三角形的面积公式可求得
中,由三角形的面积公式可求得![]() ,再利用余弦定理求出
,再利用余弦定理求出![]() ;(Ⅱ)在
;(Ⅱ)在![]() 中,由正弦定理求出
中,由正弦定理求出![]() 和
和![]() ,根据题意
,根据题意![]() 平分
平分![]() ,
, ![]() ,在
,在![]() 和
和![]() 中分别写出正弦定理,得出比例关系,求出
中分别写出正弦定理,得出比例关系,求出![]() .
.
试题解析:(I)在![]() 中,
中,
 .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 为锐角,所以
为锐角,所以![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得![]()
![]()
![]()
所以CD的长为![]() .
.
(II)在![]() 中,由正弦定理得
中,由正弦定理得![]()
即![]() ,解得
,解得![]()
![]() ,
, ![]() 也为锐角.
也为锐角.
![]() .
.
在![]() 中,由正弦定理得
中,由正弦定理得![]()
即 ![]() ①
①
在![]() 中,由正弦定理得
中,由正弦定理得![]()
即![]() ②
②
![]()
![]() 平分
平分![]() ,
, ![]()
![]()
由①②得![]() ,解得
,解得![]()
因为![]() 为锐角,所以
为锐角,所以![]() .
.
点睛: 解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:
第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.
第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化.
第三步:求结果.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+)(A>0,ω>0,||<π),在同一周期内,当 ![]() 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当 ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式和图象的对称中心;
(2)若 ![]() 时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
时,关于x的方程2f(x)+1﹣m=0有且仅有一个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于点(﹣ ![]() ,0)成中心对称,且对任意的实数x都有
,0)成中心对称,且对任意的实数x都有 ![]() ,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
A.0
B.﹣2
C.1
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=xln(﹣x)+(a﹣1)x.
(1)若f(x)在x=﹣e处取得极值,求函数f(x)的单调区间;
(2)求函数f(x)在区间[﹣e2 , ﹣e﹣1]上的最大值g(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲乙丙三辆汽车在不同速度下的燃油效率情况,下列叙述中正确的是( )
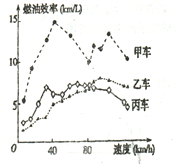
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比乙车更省油.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值.
的值.
(2)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com