
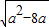 ≤3 求得8<a≤9,再根据f(4)<0,f(5)<0,f(6)≥0求得a的范围.
≤3 求得8<a≤9,再根据f(4)<0,f(5)<0,f(6)≥0求得a的范围. .
.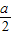 >4,设A=(m,n),由于集合A中恰有两个整数则有n-m≤3,
>4,设A=(m,n),由于集合A中恰有两个整数则有n-m≤3,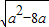 ≤3,即a2-8a≤9,解得 8<a≤9.
≤3,即a2-8a≤9,解得 8<a≤9.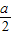 <5,而f(2)=4>0,f(3)=9-a≥0,
<5,而f(2)=4>0,f(3)=9-a≥0,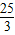 <a≤9.
<a≤9. ,或
,或 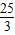 ≤a≤9.
≤a≤9.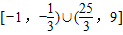 ,
,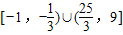 .
.

 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com