【答案】
分析:根据等差数列的前n项和的公式分别求出S
2007和S
2005的值,将其值代入到
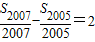
中即可求出公差d,然后根据首项为-2008,公差为2算出S
2008的值即可.
解答:解:因为S
2007=2007×(-2008)+
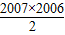
d,
S
2005=2005×(-2008)+
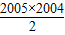
d,
则
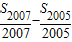
=[2007×(-2008)+
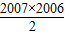
d]-[2005×(-2008)+
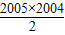
d]=2,
化简可得d=2.则S
2008=2008×(-2008)+
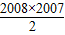
×2=2008×(-2008+2007)=-2008
故选C
点评:考查学生灵活运用等差数列的前n项和的公式化简求值,解题的关键是求数列的公差.

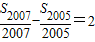 ,则S2008的值为( )
,则S2008的值为( )