
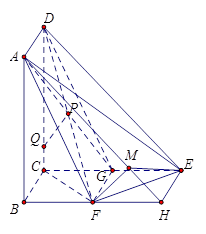
如图,已知平面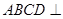 平面
平面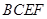 ,且四边形
,且四边形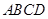 为矩形,四边形
为矩形,四边形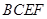 为直角梯形,
为直角梯形,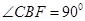 ,
,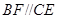 ,
,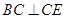 ,
,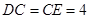 ,
,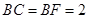 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设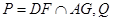 是直线
是直线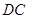 上的动点,判断并证明直线
上的动点,判断并证明直线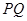 与直线
与直线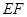 的位置关系.
的位置关系.
(3)求直线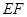 与平面
与平面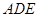 所成角的余弦值.
所成角的余弦值.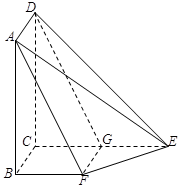
(1)见解答. (2)垂直. (3)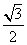 .
.
解析试题分析:(1)根据几何体在三个方向的投影即可得其三视图;(2)一般地判断两直线的位置关系,都应该从平行与垂直两个方向去考虑.在本题中,直线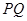 与直线
与直线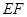 明显不平行,故朝垂直的方向考虑.连接
明显不平行,故朝垂直的方向考虑.连接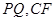 ,结合题设易得
,结合题设易得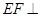 平面
平面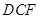 ,从而得
,从而得 .(3)结合该几何体的特征,可将面ADE补为一个矩形,这样便可作出EF在面ADE内的射影,从而求得EF与平面AED所成的角的余弦..
.(3)结合该几何体的特征,可将面ADE补为一个矩形,这样便可作出EF在面ADE内的射影,从而求得EF与平面AED所成的角的余弦..
(1)该几何体的三视图如下图所示: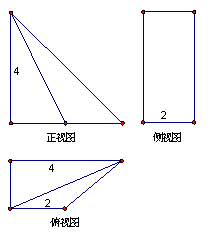
(2)连接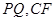 ,
,
因为 ,所以
,所以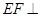 平面
平面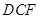 ,
,
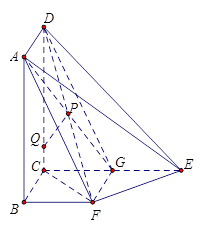
所以 .
.
(3)因为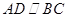 ,所以
,所以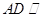 平面
平面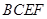 ,
,
又平面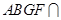 平面
平面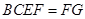 ,
,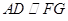 ,从而
,从而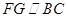 ,所以点G是CE的中点.
,所以点G是CE的中点.
过E作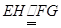 ,连接FH、AH.
,连接FH、AH.
过F作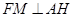 ,则
,则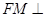 平面
平面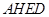 ,所以
,所以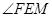 就是EF与平面AED所成的角.
就是EF与平面AED所成的角. 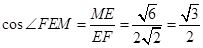 .
.
考点:1、三视图;2、空间两直线的位置关系;3、空间直线与平面所成的角.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
如图菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,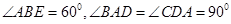 ,点H、G分别是线段EF、BC的中点.
,点H、G分别是线段EF、BC的中点.
(1)求证:平面AHC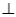 平面
平面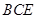 ;(2)(2)求此几何体的体积.
;(2)(2)求此几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在边长为5+ 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.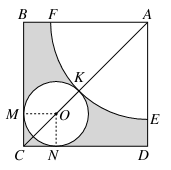
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com