
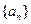 的公比为
的公比为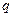 ,前
,前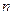 项和为
项和为 ,若
,若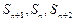 成等差数列,则
成等差数列,则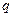 的值为 .
的值为 .科目:高中数学 来源:不详 题型:解答题
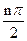 )an+sin
)an+sin ,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=
,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn= ,令 Sn=
,令 Sn= 求Sn
求Sn查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
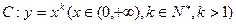 的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为
的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为 .
. 是等比数列,并求其通项公式;
是等比数列,并求其通项公式; ;(3)当
;(3)当 的前n项和Sn.
的前n项和Sn.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
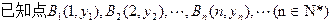
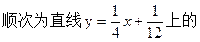 点,点A1(x1,0),A2(x
点,点A1(x1,0),A2(x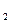 ,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x
,0),…,An(xn,0),…顺次为x轴上的点,其中x1=a(0<a≤1).对于任意n∈N*,点An、Bn、An+1构成以Bn为顶点的等腰三角形.(1)求数列{yn}的通项公式,并证明它为等差数列;(2)求证:x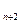 - x
- x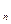 是常数,并求数列{ x
是常数,并求数列{ x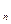 }的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.
}的通项公式;(3)上述等腰ΔAnBnAn+1中是否可能存在直角三角形,若可能,求出此时a的值;若不可能,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 项正项数列为
项正项数列为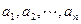 ,
,  为其前
为其前 项的积,定义
项的积,定义 为“叠乘积”.如果有2005项的正项数列
为“叠乘积”.如果有2005项的正项数列 的“叠乘积”为
的“叠乘积”为 ,则有2006项的数列
,则有2006项的数列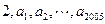 的“叠乘积”为 ( )
的“叠乘积”为 ( )A.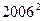 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com