练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    判断函数f(x)=lg(
    		x2+1
    -x)    的奇偶性、单调性．
    分析：首先求出函数的定义域，再由奇偶性的定义判断f（-x）和f（x）的关系，可利用奇函数的变形公式，求f（-x）+f（x）=0．然后先由导数判断y=
    		x2+1
    -x    的单调性，再由复合函数的单调性确定f（x）的单调性即可．
    解答：解：因为
    		x2+1
    ＞x    ，所以f（x）的定义域为R，
    因为f（-x）+f（x）=lg(
    		x2+1
    +x)+lg(
    		x2+1
    -x)    =lg(
    		x2+1
    +x) (
    		x2+1
    -x)    =0
    所以f（-x）=-f（x），所以f（x）为奇函数．
    令y=
    		x2+1
    -x    ，则y′=
    2x
    2
    		x2+1
    -1    ＜0，所以y=
    		x2+1
    -x    是减函数，
    由复合函数的单调性知f（x）为减函数．
    点评：本题考查复合函数的单调性和奇偶性的判断和证明，注意奇函数的变形公式f（-x）+f（x）=0
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    (2006北京朝阳模拟)已知函数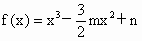，1＜m＜2．

    (1)若f(x)在区间[－1，1]上的最大值为1，最小值为－2，求m、n的值；

    (2)在(1)条件下，求经过点P（2，1）且与曲线f(x)相切的直线l的方程；

    (3)设函数f(x)的导函数为g(x)，函数，试判断函数F(x)的极值点个数，并求出相应实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源：山东省实验中学2012届高三第三次诊断性测试数学文科试题 题型：044

    已知函数f(x)的导数，a，b为实数，1＜a＜2

    (1)若f(x)在区间[－1，1]上的最小值、最大值分别为－2、1，求a、b的值；

    (2)在(1)的条件下，求经过点P(2，1)且与曲线f(x)相切的直线L的方程；

    (3)设函数，试判断函数F(x)的极值点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)在(-1,1)上有意义，f()=-1，且对任意的x、y∈(-l，1)都有f(x)+f(y)=f()．

    (1)判断函数f(x)的奇偶性；

    (2)对数列x1=(n∈N*),求f（xn）；

    (3)求证：（n∈N*）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=,x＞0.

    (1)判断函数f(x)在区间(0,+∞)上的单调性,证明你的结论;

    (2)若当x＞0时,f(x)＞恒成立,求正整数k的最大值.(参考数据:ln2≈0.7,ln3≈1.1)

    (文) P1是椭圆+y2=1(a＞0且a≠1)上不与顶点重合的任一点,P1P2是垂直于x轴的弦,A1(-a,0),A2(a,0)是椭圆的两个端点,直线A1P1与直线A2P2交点为P.

    (1)求P点的轨迹曲线C的方程;

    (2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;

    (3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且=-3,求a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)的导数f′(x)＝3x2－3ax，f(0)＝b，a，b为实数，1<a<2.

    (1)若f(x)在区间[－1,1]上的最小值、最大值分别为－2、1，求a、b的值；

    (2)在(1)的条件下，求经过点P(2,1)且与曲线f(x)相切的直线l的方程；

    (3)设函数F(x)＝[f′(x)＋6x＋1]·e2x，试判断函数F(x)的极值点个数.

    查看答案和解析>>

    同步练习册答案