
ΓΨΧβΡΩΓΩ2015Ρ–άΚ―«Ϋθ»ϋΨω»ϋΫΉΕΈΘ§÷–ΙζΡ–άΚ“‘9Ν§ ΛΒΡ≤ΜΑή’ΫΦ®”°ΒΟ28Ϋλ―«Ϋθ»ϋΙΎΨϋΘ§Ά§ ±ΡΟΒΫ―«÷όΈ®“Μ1’≈÷±Ά®άο‘ΦΑ¬‘ΥΜαΒΡ»κ≥Γ»·Θ°»ϋΚσΘ§÷–ΙζΡ–άΚ÷ςΝΠ“ΉΫ®ΝΣ»ΌβΏ±ΨΫλ―«Ϋθ»ϋ![]() Θ®Ήν”–Φέ÷Β«ρ‘±Θ©Θ§œ¬±μ «“ΉΫ®ΝΣ‘Ύ’β9≥Γ±»»ϋ÷–ΆΕάΚΒΡΆ≥ΦΤ ΐΨίΘ°
Θ®Ήν”–Φέ÷Β«ρ‘±Θ©Θ§œ¬±μ «“ΉΫ®ΝΣ‘Ύ’β9≥Γ±»»ϋ÷–ΆΕάΚΒΡΆ≥ΦΤ ΐΨίΘ°
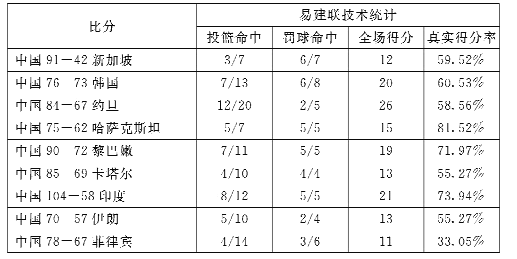
ΉΔΘΚΘ®1Θ©±μ÷–![]() ±μ Ψ≥ω ÷
±μ Ψ≥ω ÷![]() ¥ΈΟϋ÷–
¥ΈΟϋ÷–![]() ¥ΈΘΜ
¥ΈΘΜ
Θ®2Θ©![]() Θ®’φ ΒΒΟΖ÷¬ Θ© «ΚβΝΩ«ρ‘±ΫχΙΞΒΡ–ß¬ Θ§ΤδΦΤΥψΙΪ ΫΈΣΘΚ
Θ®’φ ΒΒΟΖ÷¬ Θ© «ΚβΝΩ«ρ‘±ΫχΙΞΒΡ–ß¬ Θ§ΤδΦΤΥψΙΪ ΫΈΣΘΚ
![]()
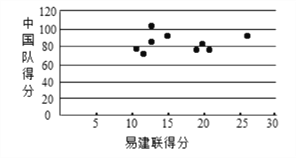
Θ®1Θ©¥”…œ ω9≥Γ±»»ϋ÷–ΥφΜζ―Γ‘ώ“Μ≥ΓΘ§«σ“ΉΫ®ΝΣ‘ΎΗΟ≥Γ±»»ϋ÷–![]() ≥§Ιΐ
≥§Ιΐ![]() ΒΡΗ≈¬ ΘΜ
ΒΡΗ≈¬ ΘΜ
Θ®2Θ©Έ“Ο«Α―±»Ζ÷Ζ÷≤ν≤Μ≥§Ιΐ15Ζ÷ΒΡ±»»ϋ≥ΤΈΣΓΑΫΚΉ≈±»»ϋΓ±.ΈΣΝΥΩΦ≤λ“ΉΫ®ΝΣ‘ΎΓΑΫΚΉ≈±»»ϋΓ±÷–ΒΡΖΔΜ”«ιΩωΘ§¥”ΓΑΫΚΉ≈±»»ϋΓ±÷–ΥφΜζ―Γ‘ώΝΫ≥ΓΘ§«σ“ΉΫ®ΝΣ‘Ύ’βΝΫ≥Γ±»»ϋ÷–![]() ÷Ν…Ό”–“Μ≥Γ≥§Ιΐ
÷Ν…Ό”–“Μ≥Γ≥§Ιΐ![]() ΒΡΗ≈¬ ΘΜ
ΒΡΗ≈¬ ΘΜ
Θ®3Θ©”Ο![]() ά¥±μ Ψ“ΉΫ®ΝΣΡ≥≥ΓΒΡΒΟΖ÷Θ§”Ο
ά¥±μ Ψ“ΉΫ®ΝΣΡ≥≥ΓΒΡΒΟΖ÷Θ§”Ο![]() ά¥±μ Ψ÷–ΙζΕ”ΗΟ≥ΓΒΡΉήΖ÷Θ§Μ≠≥ω…ΔΒψΆΦ»γΆΦΥυ ΨΘ§«κΗυΨί…ΔΒψΆΦ≈–Εœ
ά¥±μ Ψ÷–ΙζΕ”ΗΟ≥ΓΒΡΉήΖ÷Θ§Μ≠≥ω…ΔΒψΆΦ»γΆΦΥυ ΨΘ§«κΗυΨί…ΔΒψΆΦ≈–Εœ![]() ”κ
”κ![]() ÷°Φδ «ΖώΨΏ”–œΏ–‘œύΙΊΙΊœΒΘΩΫαΚœ ΒΦ ΦρΒΞΥΒΟςάμ”…Θ°
÷°Φδ «ΖώΨΏ”–œΏ–‘œύΙΊΙΊœΒΘΩΫαΚœ ΒΦ ΦρΒΞΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ;Θ®2Θ©
;Θ®2Θ©![]() ;Θ®3Θ©≤ΜΨΏ”–œΏ–‘œύΙΊΙΊœΒ.
;Θ®3Θ©≤ΜΨΏ”–œΏ–‘œύΙΊΙΊœΒ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷Έω:(1)”…“―÷Σ,ΫαΚœΙ≈ΒδΗ≈–ΆΦΤΥψΙΪ ΫΩ…ΒΟ:“ΉΫ®ΝΣ‘ΎΗΟ≥Γ±»»ϋ÷–![]() ≥§Ιΐ
≥§Ιΐ![]() ΒΡΗ≈¬ ;(2)”…“―÷Σ,ΫαΚœΙ≈ΒδΗ≈–ΆΦΤΥψΙΪ ΫΩ…ΒΟ: “ΉΫ®ΝΣ‘ΎΗΟ≥Γ±»»ϋ÷–
ΒΡΗ≈¬ ;(2)”…“―÷Σ,ΫαΚœΙ≈ΒδΗ≈–ΆΦΤΥψΙΪ ΫΩ…ΒΟ: “ΉΫ®ΝΣ‘ΎΗΟ≥Γ±»»ϋ÷–![]() ≥§Ιΐ
≥§Ιΐ![]() ΒΡΗ≈¬ ;(3)ΗυΨί…ΔΒψΆΦ,≤Δ≤Μ «Ζ÷≤Φ‘ΎΡ≥“ΜΧθ÷±œΏΒΡ÷ήΈß,Ω…ΒΟΫα¬έ.
ΒΡΗ≈¬ ;(3)ΗυΨί…ΔΒψΆΦ,≤Δ≤Μ «Ζ÷≤Φ‘ΎΡ≥“ΜΧθ÷±œΏΒΡ÷ήΈß,Ω…ΒΟΫα¬έ.
‘ΧβΫβΈω:Θ®1Θ©…η“ΉΫ®ΝΣ‘Ύ±»»ϋ÷–![]() ≥§Ιΐ
≥§Ιΐ![]() ΈΣ ¬Φΰ
ΈΣ ¬Φΰ![]() Θ§‘ρΙ≤”–8≥Γ±»»ϋ÷–
Θ§‘ρΙ≤”–8≥Γ±»»ϋ÷–![]() ≥§Ιΐ
≥§Ιΐ![]() Θ§Ι
Θ§Ι ![]() Θ§
Θ§
Θ®2Θ©…ηΓΑ“ΉΫ®ΝΣ‘Ύ’βΝΫ≥Γ±»»ϋ÷–![]() ÷Ν…Ό”–“Μ≥Γ≥§Ιΐ
÷Ν…Ό”–“Μ≥Γ≥§Ιΐ![]() Γ±ΈΣ ¬Φΰ
Γ±ΈΣ ¬Φΰ![]() Θ§‘ρ¥”…œ ω9≥Γ±»»ϋ÷–ΥφΜζ―Γ‘ώΝΫ≥ΓΙ≤”–
Θ§‘ρ¥”…œ ω9≥Γ±»»ϋ÷–ΥφΜζ―Γ‘ώΝΫ≥ΓΙ≤”–![]() ΗωΜυ±Ψ ¬ΦΰΘ§Εχ¥”÷–»Έ“β―Γ‘ώΝΫ≥Γ÷–Θ§ΝΫ≥Γ
ΗωΜυ±Ψ ¬ΦΰΘ§Εχ¥”÷–»Έ“β―Γ‘ώΝΫ≥Γ÷–Θ§ΝΫ≥Γ![]() ΕΦ≤Μ≥§Ιΐ
ΕΦ≤Μ≥§Ιΐ![]() ΒΡ”–
ΒΡ”–![]() ΗωΜυ±Ψ ¬ΦΰΘ§Ρ«Ο¥ΝΫ≥Γ÷Ν…Ό”–“Μ≥Γ≥§Ιΐ
ΗωΜυ±Ψ ¬ΦΰΘ§Ρ«Ο¥ΝΫ≥Γ÷Ν…Ό”–“Μ≥Γ≥§Ιΐ![]() ΒΡΜυ±Ψ ¬ΦΰΈΣ
ΒΡΜυ±Ψ ¬ΦΰΈΣ![]() ΗωΜυ±Ψ ¬ΦΰΘ°
ΗωΜυ±Ψ ¬ΦΰΘ°
![]() Θ°
Θ°
Θ®3Θ©≤ΜΨΏ”–œΏ–‘œύΙΊΙΊœΒΘ°“ρΈΣ…ΔΒψΆΦ≤Δ≤Μ «Ζ÷≤Φ‘ΎΡ≥“ΜΧθ÷±œΏΒΡ÷ήΈßΘ°άΚ«ρ «Φ·Χε‘ΥΕ·Θ§Ηω»ΥΈόΖ®Άξ»Ϊ÷ς‘Ή“Μ≥Γ±»»ϋΘ°


 Χτ’Ϋ100ΒΞ‘ΣΦλ≤β ‘ΨμœΒΝ–¥πΑΗ
Χτ’Ϋ100ΒΞ‘ΣΦλ≤β ‘ΨμœΒΝ–¥πΑΗ ΟϊΧβΫπΨμœΒΝ–¥πΑΗ
ΟϊΧβΫπΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4![]() 4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷Σ÷±œΏl1ΘΚ
÷–Θ§“―÷Σ÷±œΏl1ΘΚ ![]() Θ®
Θ®![]() Θ§
Θ§ ![]() Θ©Θ§≈ΉΈοœΏCΘΚ
Θ©Θ§≈ΉΈοœΏCΘΚ  Θ®tΈΣ≤Έ ΐΘ©Θ°“‘‘≠Βψ
Θ®tΈΣ≤Έ ΐΘ©Θ°“‘‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
Θ®ΔώΘ©«σ÷±œΏl1 ΚΆ≈ΉΈοœΏCΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ÷±œΏl1 ΚΆ≈ΉΈοœΏCœύΫΜ”ΎΒψAΘ®“λ”Ύ‘≠ΒψOΘ©Θ§Ιΐ‘≠ΒψΉς”κl1¥Ι÷±ΒΡ÷±œΏl2Θ§l2ΚΆ≈ΉΈοœΏCœύΫΜ”ΎΒψBΘ®“λ”Ύ‘≠ΒψOΘ©Θ§«σΓςOABΒΡΟφΜΐΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕ![]() ÷–Θ§
÷–Θ§ ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() .
.

Θ®1Θ©«σ÷ΛΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
Υυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§
Θ§ ![]() .
.
Θ®1Θ©«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©Νν![]() Θ§…η ΐΝ–
Θ§…η ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§«σ
Θ§«σ![]() ΘΜ
ΘΜ
Θ®3Θ©Νν![]() Θ§»τ
Θ§»τ![]() Ε‘
Ε‘![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
“―÷ΣΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() Θ§“‘
Θ§“‘![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§
÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§ ![]() ΒψΒΡΦΪΉχ±ξΈΣ
ΒψΒΡΦΪΉχ±ξΈΣ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©.
ΈΣ≤Έ ΐΘ©.
Θ®1Θ©–¥≥ωΒψ![]() ΒΡ÷±Ϋ«Ήχ±ξΦΑ«ζœΏ
ΒΡ÷±Ϋ«Ήχ±ξΦΑ«ζœΏ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©»τ![]() ΈΣ«ζœΏ
ΈΣ«ζœΏ![]() …œΒΡΕ·ΒψΘ§«σ
…œΒΡΕ·ΒψΘ§«σ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΘΚ
ΘΚ ![]() ΒΡΨύάκΒΡΉν–Γ÷Β.
ΒΡΨύάκΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐy=x2©¹ax©¹3Θ®©¹5ΓήxΓή5Θ©
Θ®1Θ©»τa=2Θ§«σΚ· ΐΒΡΉν÷ΒΘΜ
Θ®2Θ©»τΚ· ΐ‘ΎΕ®“ε”ρΡΎ «ΒΞΒςΚ· ΐΘ§«σa»Γ÷ΒΒΡΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΗςΉιΚ· ΐfΘ®xΘ©”κgΘ®xΘ©ΒΡΆΦœσœύΆ§ΒΡ «Θ® Θ©
A.fȮxȩ=xȧgȮxȩ=Ȯ ![]() ȩ2
Θ©2
B.fΘ®xΘ©=x2 Θ§ gΘ®xΘ©=Θ®x+1Θ©2
C.fΘ®xΘ©=1Θ§gΘ®xΘ©=x0
D.fΘ®xΘ©=|x|Θ§gΘ®xΘ©= ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Χί–Έ![]() ÷–Θ§
÷–Θ§![]() ,
,![]() «
«![]() ΒΡ÷–ΒψΘ§ΫΪ
ΒΡ÷–ΒψΘ§ΫΪ![]() ―Ί
―Ί![]() ’έΤπΘ§ ΙΒΟ
’έΤπΘ§ ΙΒΟ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
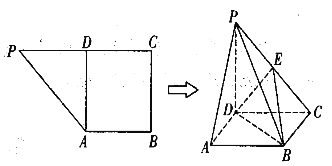
Θ®ΔώΘ©«σ÷ΛΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() «
«![]() ΒΡ÷–Βψ,«σ»ΐάβΉΕ
ΒΡ÷–Βψ,«σ»ΐάβΉΕ![]() ΒΡΧεΜΐ.
ΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβœϊΖ―’ΏΙΚΈο«ιΩωΘ§Ρ≥ΙΚΈο÷––Ρ‘ΎΒγΡ‘–ΓΤ±÷–ΥφΜζ≥ι»Γ![]() ’≈Ϋχ––Ά≥ΦΤΘ§ΫΪΫαΙϊΖ÷≥…6ΉιΘ§Ζ÷±π «ΘΚ
’≈Ϋχ––Ά≥ΦΤΘ§ΫΪΫαΙϊΖ÷≥…6ΉιΘ§Ζ÷±π «ΘΚ ![]() Θ§
Θ§ ![]() Θ§÷Τ≥…»γœ¬Υυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®ΦΌ…ηœϊΖ―ΫπΕνΨυ‘Ύ
Θ§÷Τ≥…»γœ¬Υυ ΨΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®ΦΌ…ηœϊΖ―ΫπΕνΨυ‘Ύ![]() ‘ΣΒΡ«χΦδΡΎΘ©.
‘ΣΒΡ«χΦδΡΎΘ©.
Θ®1Θ©»τ‘ΎœϊΖ―ΫπΕνΈΣ![]() ‘Σ«χΦδΡΎΑ¥Ζ÷≤ψ≥ι―υ≥ι»Γ6’≈ΒγΡ‘–ΓΤ±Θ§‘Ό¥”÷–»Έ―Γ2’≈Θ§«σ’β2’≈–ΓΤ±ά¥Ή‘
‘Σ«χΦδΡΎΑ¥Ζ÷≤ψ≥ι―υ≥ι»Γ6’≈ΒγΡ‘–ΓΤ±Θ§‘Ό¥”÷–»Έ―Γ2’≈Θ§«σ’β2’≈–ΓΤ±ά¥Ή‘![]() ‘ΣΚΆ
‘ΣΚΆ![]() ‘Σ«χΦδΘ®ΝΫ«χΦδΕΦ”–Θ©ΒΡΗ≈¬ ΘΜ
‘Σ«χΦδΘ®ΝΫ«χΦδΕΦ”–Θ©ΒΡΗ≈¬ ΘΜ
Θ®2Θ©ΈΣΉωΚΟ¥ΚΫΎΤΎΦδΒΡ…Χ≥Γ¥ΌœζΜνΕ·Θ§…Χ≥Γ…ηΦΤΝΥΝΫ÷÷≤ΜΆ§ΒΡ¥ΌœζΖΫΑΗ.

ΖΫΑΗ“ΜΘΚ»Ϊ≥Γ…ΧΤΖ¥ρΑΥΈε’έ.
ΖΫΑΗΕΰΘΚ»Ϊ≥ΓΙΚΈο¬ζ100‘ΣΦθ20‘ΣΘ§¬ζ300‘ΣΦθ80‘ΣΘ§¬ζ500‘ΣΦθ120‘ΣΘ§“‘…œΦθΟβ÷Μ»ΓΉνΗΏ”≈ΜίΘ§≤Μ÷ΊΗ¥ΦθΟβ.άϊ”Ο÷±ΖΫΆΦΒΡ–≈œΔΖ÷ΈωΘΚΡΡ÷÷ΖΫΑΗ”≈ΜίΝΠΕ»Ηϋ¥σΘ§≤ΔΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com