
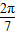 (参考数据:tan
(参考数据:tan
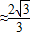 ).今计划建一个生活垃圾中转站P,为方便运输,P准备建在线段AO(不含端点)上.
).今计划建一个生活垃圾中转站P,为方便运输,P准备建在线段AO(不含端点)上.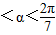 ),试将P到三个小区的距离之和y表示为a的函数,并确定当a取何值时,可使y最小?
),试将P到三个小区的距离之和y表示为a的函数,并确定当a取何值时,可使y最小?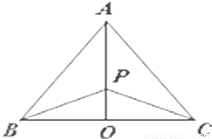
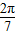 ,∴
,∴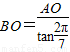 =
=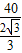 =
=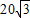 ,
,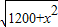 ,
,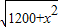 ,即0<x≤5时,S=40-x;
,即0<x≤5时,S=40-x;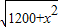 ,即5<x<40时,S=
,即5<x<40时,S=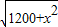 .
.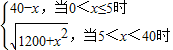 .
.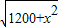 ,是增函数,∴S>S(5)=35.
,是增函数,∴S>S(5)=35.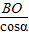 =
=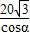 ,PO=BOtanα=
,PO=BOtanα=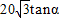 ,
,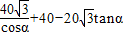 =40+
=40+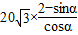
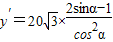 ,令y′=0,即
,令y′=0,即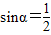 ,从而
,从而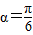 ,
,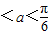 时,y′<0;当
时,y′<0;当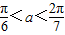 时,y′>0.
时,y′>0.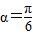 时,可使y最小.
时,可使y最小.

科目:高中数学 来源: 题型:
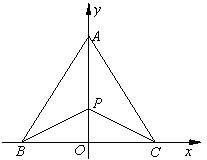 有三个生活小区,分别位于A,B,C三点处,且AB=AC=20
有三个生活小区,分别位于A,B,C三点处,且AB=AC=20| 7 |
| 3 |
| 2 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=
如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=| 2π |
| 7 |
| 2π |
| 7 |
2
| ||
| 3 |
| 2π |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
 有三个生活小区,分别位于
有三个生活小区,分别位于![]() 三点处,且
三点处,且![]() ,
,![]() . 今计划合建一个变电站,为同时方便三个小区,准备建在
. 今计划合建一个变电站,为同时方便三个小区,准备建在![]() 的垂直平分线
的垂直平分线
上的![]() 点处,建立坐标系如图,且
点处,建立坐标系如图,且![]() .
.
(Ⅰ) 若希望变电站![]() 到三个小区的距离和最小,
到三个小区的距离和最小,
点![]() 应位于何处?
应位于何处?
(Ⅱ) 若希望点![]() 到三个小区的最远距离为最小,
到三个小区的最远距离为最小,
点![]() 应位于何处?
应位于何处?
![]()
查看答案和解析>>
科目:高中数学 来源:2013届江苏盐城明达中学高三上学期学情调研考试数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,有三个生活小区(均可看成点)分别位于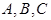 三点处,
三点处,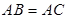 ,
,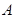 到线段
到线段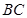 的距离
的距离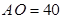 ,
,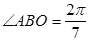 (参考数据:
(参考数据: 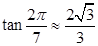 ). 今计划建一个生活垃圾中转站
). 今计划建一个生活垃圾中转站 ,为方便运输,
,为方便运输, 准备建在线段
准备建在线段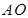 (不含端点)上.
(不含端点)上.

(1)设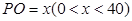 ,试将
,试将 到三个小区距离的最远者
到三个小区距离的最远者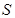 表示为
表示为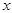 的函数,并求
的函数,并求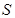 的最小值;
的最小值;
(2)设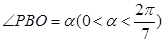 ,试将
,试将 到三个小区的距离之和
到三个小区的距离之和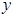 表示为
表示为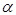 的函数,并确定当
的函数,并确定当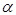 取何值时,可使
取何值时,可使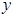 最小?
最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com