
【题目】已知椭圆C1: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,P(﹣2,1)是C1上一点.
,P(﹣2,1)是C1上一点.
(1)求椭圆C1的方程;
(2)设A,B,Q是P分别关于两坐标轴及坐标原点的对称点,平行于AB的直线l交C1于异于P、Q的两点C,D,点C关于原点的对称点为E.证明:直线PD、PE与y轴围成的三角形是等腰三角形.
【答案】
(1)解:由题意可得e= ![]() =
= ![]() ,且a2﹣b2=c2,
,且a2﹣b2=c2,
将P(﹣2,1)代入椭圆方程可得 ![]() =1,
=1,
解得a=2 ![]() ,b=
,b= ![]() ,c=
,c= ![]() ,
,
即有椭圆方程为 ![]()
(2)解:证明:A,B,Q是P(﹣2,1)分别关于两坐标轴及坐标原点的对称点,
可设A(﹣2,﹣1),B(2,1),Q(2,﹣1),
直线l的斜率为k= ![]() ,设直线l的方程为y=
,设直线l的方程为y= ![]() x+t,
x+t,
代入椭圆x2+4y2=8,可得x2+2tx+2t2﹣4=0,
设C(x1,y1),D(x2,y2),E(﹣x1,﹣y1),
即有△=4t2﹣4(2t2﹣4)>0,解得﹣2<t<2,
x1+x2=﹣2t,x1x2=2t2﹣4,
设直线PD,PE的斜率为k1,k2,
则k1+k2= ![]() +
+ ![]() =
= ![]() ,
,
要证直线PD、PE与y轴围成的三角形是等腰三角形,
只需证k1+k2=0,即(2﹣x1)(y2﹣1)﹣(2+x2)(y1+1)=0,
由y1= ![]() x1+t,y2=
x1+t,y2= ![]() x2+t,
x2+t,
可得(2﹣x1)(y2﹣1)﹣(2+x2)(y1+1)=2(y2﹣y1)﹣(x1y2+x2y1)+x1﹣x2﹣4
=x2﹣x1﹣(x1x2+tx1+tx2)+x1﹣x2﹣4=﹣x1x2﹣t(x1+x2)﹣4
=﹣(2t2﹣4)+2t2﹣4=0,
则直线PD、PE与y轴围成的三角形是等腰三角形
【解析】(1)运用椭圆的离心率公式和P满足椭圆方程,解得a,b,进而得到椭圆方程;(2)设A(﹣2,﹣1),B(2,1),Q(2,﹣1),设直线l的方程为y= ![]() x+t,代入椭圆方程,设C(x1 , y1),D(x2 , y2),E(﹣x1 , ﹣y1),运用韦达定理,设直线PD,PE的斜率为k1 , k2 , 要证直线PD、PE与y轴围成的三角形是等腰三角形,只需证k1+k2=0,化简整理,代入韦达定理,即可得证.
x+t,代入椭圆方程,设C(x1 , y1),D(x2 , y2),E(﹣x1 , ﹣y1),运用韦达定理,设直线PD,PE的斜率为k1 , k2 , 要证直线PD、PE与y轴围成的三角形是等腰三角形,只需证k1+k2=0,化简整理,代入韦达定理,即可得证.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】定义在[0,+∞)上的函数f(x)满足:①当x∈[1,2)时, ![]() ;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若
;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若 ![]() ,则x1+x2+…+x2n= .
,则x1+x2+…+x2n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , Sn=n2+2n,bn=anan+1cos(n+1)π,数列{bn} 的前n项和为Tn , 若Tn≥tn2对n∈N*恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,异面直线
,异面直线![]() 和
和![]() 所成角等于
所成角等于![]() .
.
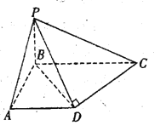
(1)求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的正切值为
所成锐二面角的正切值为![]() ?若存在,指出点
?若存在,指出点![]() 在棱
在棱![]() 上的位置;若不存在,说明理由.
上的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前不久商丘市因环境污染严重被环保部约谈后,商丘市近期加大环境治理力度,如表提供了商丘某企业节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.

(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(2)已知该企业技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)参考公式:![]() =
= ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆 ![]() 的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线
的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线 ![]() 与椭圆E有且仅有一个交点M. (Ⅰ)求椭圆E的方程;
与椭圆E有且仅有一个交点M. (Ⅰ)求椭圆E的方程;
(Ⅱ)设直线 ![]() 与y轴交于P,过点P的直线与椭圆E交于两不同点A,B,若λ|PM|2=|PA||PB|,求实数λ的取值范围.
与y轴交于P,过点P的直线与椭圆E交于两不同点A,B,若λ|PM|2=|PA||PB|,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com