
【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12. 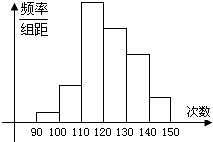
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 .
【答案】
(1)解:∵从左到右各小长方形的面积之比为2:4:17:15:9:3,
第二小组频数为12.
∴样本容量是 ![]() =150,
=150,
∴第二小组的频率是 ![]() =0.08.
=0.08.
(2)解:∵次数在110以上为达标,
∴在这组数据中达标的个体数一共有17+15+9+3,
∴全体学生的达标率估计是 ![]() =0.88
=0.88
(3)115;121.3
【解析】解:(3)在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数,
即 ![]() =115,
=115,
处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数121.3
【考点精析】本题主要考查了频率分布直方图和平均数、中位数、众数的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据才能正确解答此题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】对一批底部周长属于[80,130](单位:cm)的树木进行研究,从中随机抽出200株树木并测出其底部周长,得到频率分布直方图如图所示,由此估计,这批树木的底部周长的众数是cm,中位数是cm,平均数是cm. 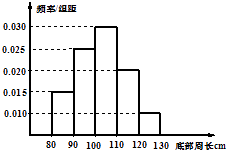
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 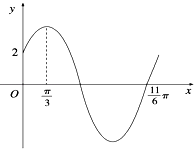
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ![]() ,
, ![]() ]时,求函数y=f(x+
]时,求函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com