
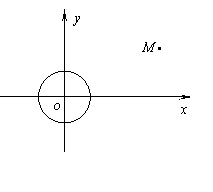
 已知⊙
已知⊙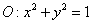 和点
和点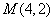 .
.
(Ⅰ)过点 向⊙
向⊙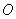 引切线
引切线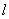 ,求直线
,求直线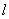 的方程;
的方程;
(Ⅱ)求以点 为圆心,且被直线
为圆心,且被直线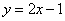 截得的弦长为 4的⊙
截得的弦长为 4的⊙ 的方程;
的方程;
(Ⅲ)设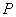 为(Ⅱ)中⊙
为(Ⅱ)中⊙ 上任一点,过点
上任一点,过点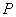 向⊙
向⊙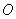 引切线,切点为Q. 试探究:平面内是否存在一定点
引切线,切点为Q. 试探究:平面内是否存在一定点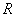 ,使得
,使得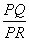 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
解:(Ⅰ)设切线 方程为
方程为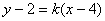 ,易得
,易得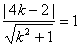 ,解得
,解得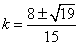 ……3分
……3分
∴切线 方程为
方程为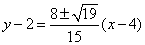 ………………………………………………………5分
………………………………………………………5分
(Ⅱ)圆心到直线 的距离为
的距离为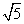 …………………………7分
…………………………7分
设圆的半径为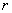 ,则
,则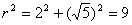 ………………………………………………9分
………………………………………………9分
∴⊙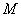 的方程为
的方程为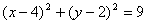 ………………………………………………… 10分
………………………………………………… 10分
(Ⅲ)假设存在这样的点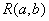 ,点
,点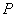 的坐标为
的坐标为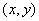 ,相应的定值为
,相应的定值为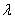 ,
,
根据题意可得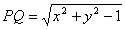 ,∴
,∴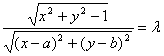 …………………………12分
…………………………12分
即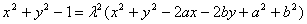 (*),
(*),
又点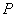 在圆上∴
在圆上∴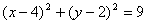 ,即
,即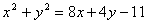 ,代入(*)式得:
,代入(*)式得:
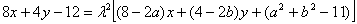 ………………………………14分
………………………………14分
若系数对应相等,则等式恒成立,∴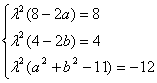 ,
,
解得 ,
,
∴可以找到这样的定点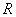 ,使得
,使得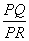 为定值. 如点
为定值. 如点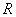 的坐标为
的坐标为 时,比值为
时,比值为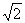 ;
;
点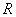 的坐标为
的坐标为 时,比值为
时,比值为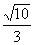 …………………………………………………………16分
…………………………………………………………16分


科目:高中数学 来源: 题型:
已知函数![]() 和点
和点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
(Ⅰ)设![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅱ)是否存在![]() ,使得
,使得![]() 、
、![]() 与
与![]() 三点共线.若存在,求出
三点共线.若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内总存在
内总存在![]() 个实数
个实数![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,求
成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高一第二学期期中考试数学试卷(解析版) 题型:选择题
已知△ABC和点M满足 ,若存在实数m,使得
,若存在实数m,使得
 ,则m=( )
,则m=( )
A、2 B、3 C、4 D、5
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一下学期期中考试数学(5-7班) 题型:解答题
(本题满分15分)已知射线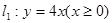 和点
和点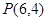 ,试在
,试在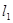 上求一点
上求一点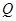 使得
使得 所在直线
所在直线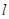 和
和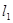 、直线
、直线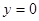 在第一象限围成的面积达到最小值,并写出此时直线
在第一象限围成的面积达到最小值,并写出此时直线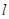 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一下学期期中考试数学(1-4班) 题型:解答题
已知射线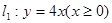 和点
和点 ,试在
,试在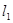 上求一点
上求一点 使得
使得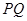 所在直线
所在直线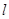 和
和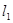 ,直线
,直线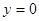 在第一象限围成的三角形面积达到最小值,并写出此时直线
在第一象限围成的三角形面积达到最小值,并写出此时直线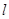 的方程。
的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com