
【题目】已知在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
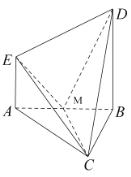
(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正切值为2,求二面角
所成角的正切值为2,求二面角![]() 的大小.
的大小.
科目:高中数学 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,古代用它作为长方体棱台(上、下底面均为矩形额棱台)的专用术语,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上表,下表从之,亦倍小表,上表从之,各以其广乘之,并,以高若深乘之,皆六面一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘;将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一,以此算法,现有上下底面为相似矩形的棱台,相似比为![]() ,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:kx-y+4=0与直线l2:x+ky-3=0相交于点P,则当实数k变化时,点P到直线4x-3y+10=0的距离的最大值为( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() 是正实数,当
是正实数,当![]() 时,
时,![]() ,则称
,则称![]() 是“
是“![]() -数列”.已知数列
-数列”.已知数列![]() 是“
是“![]() -数列”.
-数列”.
(Ⅰ)若![]() ,写出
,写出![]() 的所有可能值;
的所有可能值;
(Ⅱ)证明:![]() 是等差数列当且仅当
是等差数列当且仅当![]() 单调递减;
单调递减;
(Ⅲ)若存在正整数![]() ,对任意正整数
,对任意正整数![]() ,都有
,都有![]() ,证明:
,证明:![]() 是数列
是数列![]() 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆的标准方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() ,求
,求![]() 的单调区间;并证明:当
的单调区间;并证明:当![]() 时,
时,![]() ;
;
(3)证明:当![]() 时,函数
时,函数 有最小值,设
有最小值,设![]() 最小值为
最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com