
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的斜率为2,求函数
处的切线的斜率为2,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在区间
在区间![]() 上有零点,求实数
上有零点,求实数![]() 的取值范围.(
的取值范围.(![]() 是自然对数的底数,
是自然对数的底数,![]() )
)
【答案】(1)函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() (2)
(2)![]()
【解析】
(1)求导,由导数的结合意义可求得![]() ,进而得到函数解析式,再解关于导函数的不等式即可得到单调区间;
,进而得到函数解析式,再解关于导函数的不等式即可得到单调区间;
(2)对![]() 进行分类讨论,利用导数,结合零点的存在性定理建立不等式即可求解.
进行分类讨论,利用导数,结合零点的存在性定理建立不等式即可求解.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,
,
则![]() ,所以
,所以![]() ,
,
此时![]() ,定义域为
,定义域为![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ;
;
所以函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)函数![]() 在区间
在区间![]() 上的图象是一条不间断的曲线.
上的图象是一条不间断的曲线.
由(1)知![]() ,
,
1)当![]() 时,对任意
时,对任意![]() ,
,![]() ,
,![]() ,则
,则![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,此时对任意
上单调递增,此时对任意![]() ,都有
,都有![]() 成立,从而函数
成立,从而函数![]() 在区间
在区间![]() 上无零点;
上无零点;
2)当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,其中
,其中![]() ,
,
①若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减,由题意得
上单调递减,由题意得![]() ,且
,且![]() ,解得
,解得![]() ,其中
,其中![]() ,即
,即![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() ;
;
②若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增,此时对任意
上单调递增,此时对任意![]() ,都有
,都有![]() 成立,从而函数
成立,从而函数![]() 在区间
在区间![]() 上无零点;
上无零点;
③若![]() ,即
,即![]() ,则对任意
,则对任意![]() ,
,![]() ;所以函数
;所以函数![]() 在区间
在区间![]() 上单调递增,对任意
上单调递增,对任意![]() ,都有
,都有![]() 成立;
成立;
对任意![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减,由题意得
上单调递减,由题意得
![]() ,解得
,解得![]() ,
,
其中![]() ,即
,即![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() .
.
综上可得,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意可求得![]() ,则
,则![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
当直线![]() 的斜率不存在或直线
的斜率不存在或直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,结合韦达定理计算可得直线
,联立直线方程与椭圆方程,结合韦达定理计算可得直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .综上可得:直线
.综上可得:直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(Ⅰ)设![]() 由题
由题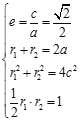 ,
,
解得![]() ,则
,则![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,
设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
可得![]()
![]() ,
,![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,
则由 消去
消去![]() 可得:
可得:![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得:
,代入上述方程可得:
![]() ,
,![]() ,
,
则![]()
![]() ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]()
 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【点睛】
(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
【题型】解答题
【结束】
21
【题目】已知函数f(x)=(x+b)(![]() -a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
-a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(Ⅰ)求a,b;
(Ⅱ)若方程f(x)=m有两个实数根x1,x2,且x1<x2,证明:x2-x1≤1+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水稻就是耐盐碱水稻,是一种介于野生稻和栽培稻之间的普遍生长在海边滩涂地区的水稻,具有抗旱抗涝、抗病虫害、抗倒伏抗盐碱等特点.近年来,我国的海水稻研究取得了阶段性成果,目前已开展了全国大范围试种.某农业科学研究所分别抽取了试验田中的海水稻以及对照田中的普通水稻各![]() 株,测量了它们的根系深度(单位:
株,测量了它们的根系深度(单位:![]() ),得到了如下的茎叶图,其中两竖线之间表示根系深度的十位数,两边分别是海水稻和普通水稻根系深度的个位数,则下列结论中不正确的是( )
),得到了如下的茎叶图,其中两竖线之间表示根系深度的十位数,两边分别是海水稻和普通水稻根系深度的个位数,则下列结论中不正确的是( )
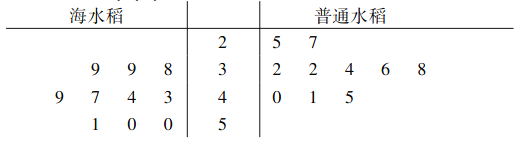
A.海水稻根系深度的中位数是![]()
B.普通水稻根系深度的众数是![]()
C.海水稻根系深度的平均数大于普通水稻根系深度的平均数
D.普通水稻根系深度的方差小于海水稻根系深度的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象是自原点出发的一条折线,当
的图象是自原点出发的一条折线,当![]() (
(![]() )时,该图象是斜率为
)时,该图象是斜率为![]() 的线段,其中常数
的线段,其中常数![]() 且
且![]() ,数列
,数列![]() 由
由![]() (
(![]() )定义.
)定义.
(1)若![]() ,求
,求![]() ,
,![]() ;
;
(2)求![]() 的表达式及
的表达式及![]() 的解析式(不必求
的解析式(不必求![]() 的定义域);
的定义域);
(3)当![]() 时,求
时,求![]() 的定义域,并证明
的定义域,并证明![]() 的图象与
的图象与![]() 的图象没有横坐标大于1的公共点.
的图象没有横坐标大于1的公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆的一个顶点,△
是椭圆的一个顶点,△![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上一动点,求线段
上一动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 分别作直线
分别作直线![]() ,
,![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为![]() ,
,![]() ,
,
且![]() ,探究:直线
,探究:直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
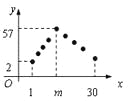
【题目】某专卖店销售一新款服装,日销售量(单位为件)f(n) 与时间n(1≤n≤30、n![]() N*)的函数关系如下图所示,其中函数f(n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
N*)的函数关系如下图所示,其中函数f(n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f(n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左右焦点分别是
的左右焦点分别是![]()
![]() ,
,![]() 是椭圆外的动点,满足
是椭圆外的动点,满足![]() .点
.点![]() 是线段
是线段![]() 与该椭圆的交点,点
与该椭圆的交点,点![]() 在线段
在线段![]() 上,并且满足
上,并且满足![]() ,
,![]() .
.
(1)当![]() 时,用点P的横坐标
时,用点P的横坐标![]() 表示
表示![]() ;
;
(2)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)在点![]() 的轨迹
的轨迹![]() 上,是否存在点
上,是否存在点![]() ,使
,使![]() 的面积
的面积![]() ?若存在,求出
?若存在,求出![]() 的正切值;若不存在,说明理由.
的正切值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
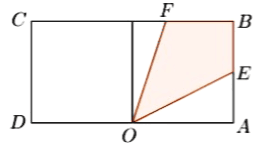
【题目】如图一块长方形区域![]() ,
,![]() ,
,![]() ,在边
,在边![]() 的中点
的中点![]() 处有一个可转动的探照灯,其照射角
处有一个可转动的探照灯,其照射角![]() 始终为
始终为![]() ,设
,设![]() ,探照灯照射在长方形
,探照灯照射在长方形![]() 内部区域的面积为
内部区域的面积为![]() .
.
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(3)若探照灯每9分钟旋转“一个来回”(![]() 自
自![]() 转到
转到![]() ,再回到
,再回到![]() ,称“一个来回”,忽略
,称“一个来回”,忽略![]() 在
在![]() 及
及![]() 处所用的时间),且转动的角速度大小一定,设
处所用的时间),且转动的角速度大小一定,设![]() 边上有一点
边上有一点![]() ,且
,且![]() ,求点
,求点![]() 在“一个来回”中被照到的时间.
在“一个来回”中被照到的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com