
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,将直线
,将直线![]() 绕极点
绕极点![]() 逆时针旋转
逆时针旋转![]() 个单位得到直线
个单位得到直线![]() .
.
(1)求![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.
对收回的100份有效问卷进行统计,得到如下2×2列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 |
|
|
女 |
| 15 |
|
合计 |
|
| 100 |
(1)求上表中的x
(2)若在犯错误的概率不超过P的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的P的值应为多少?
附:独立性检验统计量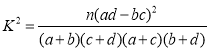 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: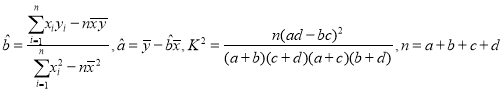 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
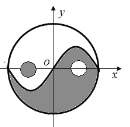
【题目】太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆![]() 被
被![]() 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为
的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为![]() ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
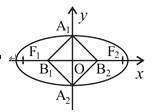
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com