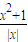练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数f（x）=1g（x≠0，x∈R），有下列命题：
    ①f（x）的图象关于y轴对称；  
    ②f（x）的最小值是2；
    ③f（x）在（-∞，0）上是减函数，在（0，+∞）上是增函数；   
    ④f（x）没有最大值．
    其中正确命题的序号是    ．（请填上所有正确命题的序号）
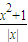    【答案】分析：①f（-x）=1g=f（x），函数f（x）是偶函数；
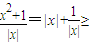    ②利用基本不等式，可得2，从而f（x）=1g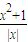≥lg2；
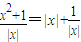    ③考查函数g（x）=的单调性，即可得到结论；
    ④由③知，f（x）没有最大值．
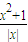    解答：解：①f（-x）=1g=f（x），∴函数f（x）是偶函数，f（x）的图象关于y轴对称，故①正确；
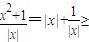    ②2，∴f（x）=1g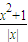≥lg2，∴f（x）的最小值是lg2，故②不正确；
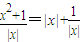    ③函数g（x）=在（-∞，-1），（0，1）上是减函数，在（-1，0），（1，+∞）上是增函数，故函数f（x）=1g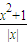在（-∞，-1），（0，1）上是减函数，在（-1，0），（1，+∞）上是增函数，故③不正确；
    ④由③知，f（x）没有最大值，故④正确
    故答案为：①④
    点评：本题考查命题的真假判断，考查学生分析解决问题的能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•泰州二模）已知函数f（x）=-x3+x2，g（x）=alnx，a∈R．
    （1）若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求a的取值范围；
    （2）设F（x）=
    f(x)，x＜1
    g(x)，x≥1
    若P是曲线y=F（x）上异于原点O的任意一点，在曲线y=F（x）上总存在另一点Q，使得△POQ中的∠POQ为钝角，且PQ的中点在y轴上，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•泸州模拟）设函数f(x)=loga
    1+x
    1-x
    (a＞0且a≠1)    ．
    （I）求f(m)+f(n)-f(
    m+n
    1+mn
    )    的值；
    （II）若关于x的方程loga
    t
    (1-x)(2x2-5x+5)
    =f(x)    在x∈[0，1）上有实数解，求实数t的取值范围．
    （III）设函数g（x）是函数f（x）的反函数，求证：当a＞1时，
    n
    k=1
    g(a-k)＜
    lna
    2(a-1)
    (n∈N*)．    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

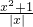    函数f（x）=1g数学公式（x≠0，x∈R），有下列命题：
    ①f（x）的图象关于y轴对称；　
    ②f（x）的最小值是2；
    ③f（x）在（-∞，0）上是减函数，在（0，+∞）上是增函数；　
    ④f（x）没有最大值．
    其中正确命题的序号是________．（请填上所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年辽宁省本溪一中、庄河高中联考高三（上）期末数学试卷（理科）（解析版） 题型：填空题

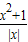    函数f（x）=1g（x≠0，x∈R），有下列命题：
    ①f（x）的图象关于y轴对称；  
    ②f（x）的最小值是2；
    ③f（x）在（-∞，0）上是减函数，在（0，+∞）上是增函数；   
    ④f（x）没有最大值．
    其中正确命题的序号是    ．（请填上所有正确命题的序号）

    查看答案和解析>>

    同步练习册答案