练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知

       （1）求表达式；

       （2）求的值，并求此时与的夹角。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知某海滨浴场的海浪高度y（单位：米）与时间 t（0≤t≤24）（单位：时）的函数关系记作y=f（t），下表是某日各时的浪高数据：
    t/时 0 3 6 9 12 15 18 21 24
    y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
    经长期观测，函数y=f（t）可近似地看成是函数y=Acosωt+b．
    （1）根据以上数据，求出函数y=Acosωt+b的最小正周期T及函数表达 式（其中A＞0，ω＞0）；
    （2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放？

    查看答案和解析>>

    科目：高中数学 来源： 题型：阅读理解

    （2013•甘肃三模）在某大学自主招生考试中，所有选报 II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A，B，C，D，E五个等级．某考场考生的两科考试成绩的数据统计如图所示，其中“数学与逻辑”科目的成绩为B的考生有10人．

    （ I）求该考场考生中“阅读与表达”科目中成绩为A的人数；
    （ II）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分，求该考场考生“数学与逻辑”科目的平均分；
    （Ⅲ）已知参加本考场测试的考生中，恰有两人的两科成绩均为A．在至少一科成绩为A的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为A的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题满分14分）

       如图所示，已知曲线交于点O、A，直线

    与曲线、分别交于点D、B，连结OD，DA，AB.

    （1）求证:曲边四边形ABOD（阴影部分：OB

    为抛物线弧）的面积的函数表达

    式为

    （2）求函数在区间上的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知某海滨浴场的海浪高度（单位：米）与时间 （单位：时）的函数关系记作，下表是某日各时的浪高数据：

    /时

    0

    3

    6

    9

    12

    15

    18

    21

    24

    /米

    1.5

    1.0

    0.5

    1.0

    1.5

    1.0

    0.5

    0.99

    1.5

    经长期观测，函数可近似地看成是函数．

    （1）根据以上数据，求出函数的最小正周期T及函数表达 式(其中);

    （2）根据规定，当海浪高度不低于0.75米时，才对冲浪爱好者开放，请根据以上结论，判断一天内从上午7时至晚上19时之间，该浴场有多少时间可向冲浪爱好者开放？

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年山东省青岛市高三3月统一质量检测考试（第二套）文科数学试卷（解析版） 题型：解答题

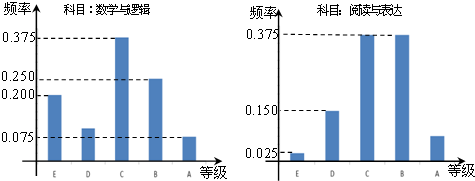
    在某高校自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为五个等级. 某考场考生的两科考试成绩数据统计如下图所示，其中“数学与逻辑”科目的成绩为的考生有人.

    （1）求该考场考生中“阅读与表达”科目中成绩为的人数；

    （2）若等级分别对应分,分,分,分,分,求该考场考生“数学与逻辑”科目的平均分；

    （3）已知参加本考场测试的考生中，恰有两人的两科成绩均为. 在至少一科成绩为的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为的概率.

     

    查看答案和解析>>

    同步练习册答案