
【题目】已知函数![]() ,其中e是自然对数的底数,
,其中e是自然对数的底数,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,讨论函数
,讨论函数![]() 零点的个数,并说明理由.
零点的个数,并说明理由.
【答案】(1)增区间是![]() ,减区间是
,减区间是![]() .(2)见解析
.(2)见解析
【解析】
(1)求导函数![]() ,分别令
,分别令![]() ,解出不等式,即可得到函数
,解出不等式,即可得到函数![]() 的单调区间;
的单调区间;
(2)由![]() 得方程
得方程 ![]() ,显然
,显然 ![]() 为此方程的一个实数解.当
为此方程的一个实数解.当![]() 时, 方程可化简为
时, 方程可化简为![]() ,设函数
,设函数![]() 利用导数得到
利用导数得到 ![]() 的最小值, 因为
的最小值, 因为![]() ,再对
,再对![]() 讨论,得到函数
讨论,得到函数![]() 的零点个数.
的零点个数.
解:(1)因为![]() ,所以
,所以![]() .
.
由![]() 得
得![]() ;由
;由![]() 得
得![]() .
.
所以由![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(2)因为![]() .
.
由![]() ,得
,得![]() 或
或![]() .
.
设![]() ,又
,又![]() 即
即![]() 不是
不是![]() 的零点,
的零点,
故只需再讨论函数![]() 零点的个数.
零点的个数.
因为![]() ,
,
所以当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
①当![]() 即
即![]() 时,无零点;
时,无零点;
②当![]() 即
即![]() 时,
时, ![]() 有唯一零点;
有唯一零点;
③当![]() ,即
,即![]() 时,因为
时,因为![]() ,
,
所以![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
令![]() 则
则![]() .
.
设![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以,![]() 都有
都有![]() .
.
所以![]() .
.
所以![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
所以当![]() 时,
时,![]() 有两个零点
有两个零点
综上所述,当![]() 时,
时,![]() 有一个零点;
有一个零点;
当![]() 时,
时,![]() 有两个零点;
有两个零点;
当![]() 时,
时,![]() 有三个零点.
有三个零点.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】小王于2015年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还贷方式,且截止2019年底,他没有再购买第二套房子.下图是2016年和2019年小王的家庭收入用于各项支出的比例分配图,根据以上信息,判断下列结论中正确的是( )
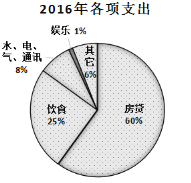
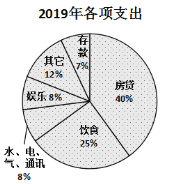
A.小王一家2019年用于饮食的支出费用跟2016年相同
B.小王一家2019年用于其他方面的支出费用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了1倍
D.小王一家2019年用于房贷的支出费用比2016年减少了
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 上一点,以点
上一点,以点![]() 及椭圆的左、右焦点
及椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形面积为
为顶点的三角形面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作斜率存在且互相垂直的直线
作斜率存在且互相垂直的直线![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 两交点的中点,
两交点的中点,![]() 是
是![]() 与
与![]() 两交点的中点,求△
两交点的中点,求△![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为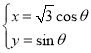 (
(![]() 为参数),在以原点O为极点,x的非负半轴为极轴建立的极坐标系中,直线
为参数),在以原点O为极点,x的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与x轴,y轴分别交于A,B两点,点P是曲线
与x轴,y轴分别交于A,B两点,点P是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形理论是当今世界十分风靡和活跃的新理论、新学科.其中把部分与整体以某种方式相似的形体称为分形.分形是一种具有自相似特性的现象.图象或者物理过程.标准的自相似分形是数学上的抽象,迭代生成无限精细的结构.也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已.谢尔宾斯基三角形就是一种典型的分形,是由波兰数学家谢尔宾斯基在1915年提出的,其构造方法如下:取一个实心的等边三角形(如图1),沿三边的中点连线,将它分成四个小三角形,挖去中间的那一个小三角形(如图2),对其余三个小三角形重复上述过程(如图3).若图1(阴影部分)的面积为1,则图4(阴影部分)的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中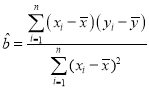 ,
,![]() .相关系数
.相关系数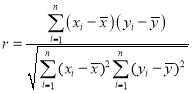 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c均为正数,设函数f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函数f(x)的最大值为1,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,P为线段
中,P为线段![]() 上的动点,下列说法正确的是( )
上的动点,下列说法正确的是( )
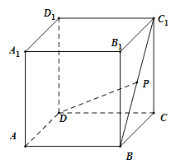
A.对任意点P,![]() 平面
平面![]()
B.三棱锥![]() 的体积为
的体积为![]()
C.线段DP长度的最小值为![]()
D.存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com