
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() .
.
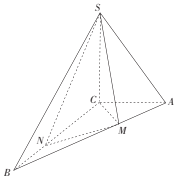
(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)证明BC⊥平面SAC,即可推出SC⊥平面ABC,从而得到MN⊥平面SCM,即可证明MN⊥SM.(2)以C为原点,以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,求出平面SAM和平面SMN的法向量,利用空间向量的夹角的余弦,求解二面角A﹣SM﹣N的余弦值.
,求出平面SAM和平面SMN的法向量,利用空间向量的夹角的余弦,求解二面角A﹣SM﹣N的余弦值.
(1)证明:由![]() ,
,![]() ,且
,且![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ,又
,又![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,故
,故![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,则
,则![]() .
.
(2)解:由(1)知,![]() ,
,![]() ,
,![]() 两两相互垂直,
两两相互垂直,
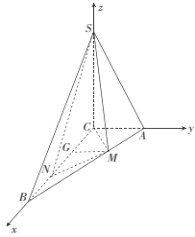
如图是以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,令
,令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,故
,故![]() .
.
所以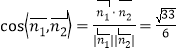 ,
,
由图可知二面角![]() 为钝角,
为钝角,
故二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
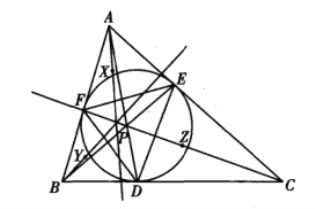
【题目】如图,△ABC的内切圆分别与边BC、CA、AB切于点D、E、F,AD与BE交于点P,设点P关于直线EF、FD、DE的对称点分别X、Y、Z.证明:AX、BY、CZ三线共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若非负整数m、n在求和时恰进位一次(十进制下),则称有序数对(m、n)为“好的”,那么,所有和为2014的好的有序数对的个数为__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() ,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,e]上的极值和最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
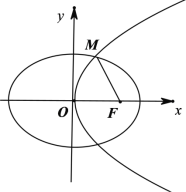
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,三角形
,三角形![]() 的两条边
的两条边![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(I)求点![]() 的轨迹方程;
的轨迹方程;
(II)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 面积
面积![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异;
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于![]() (单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
(单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
参考公式: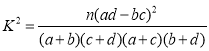 ,其中
,其中![]() .
.
参考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com