
已知数列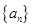 具有性质:①
具有性质:①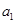 为整数;②对于任意的正整数
为整数;②对于任意的正整数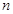 ,当
,当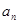 为偶数时,
为偶数时,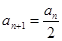 ;当
;当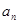 为奇数时,
为奇数时,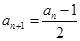 .
.
(1)若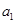 为偶数,且
为偶数,且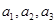 成等差数列,求
成等差数列,求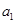 的值;
的值;
(2)设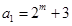 (
(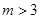 且
且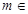 N),数列
N),数列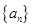 的前
的前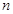 项和为
项和为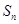 ,求证:
,求证: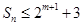 ;
;
(3)若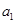 为正整数,求证:当
为正整数,求证:当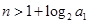 (
(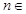 N)时,都有
N)时,都有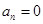 .
.
(1) 0或2;(2)证明见试题解析;(3)证明见试题解析.
解析试题分析:(1)根据数列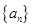 具有性质,
具有性质,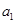 为偶数,
为偶数,
 要,这时要求
要,这时要求 ,必须讨论
,必须讨论 的奇偶性,分类讨论;(2)要证不等式
的奇偶性,分类讨论;(2)要证不等式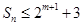 ,最好能求出
,最好能求出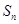 ,那么也就要求出数列
,那么也就要求出数列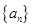 的各项,那么我们根据数列
的各项,那么我们根据数列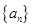 定义,由
定义,由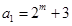 为奇数,则
为奇数,则 为奇数,
为奇数, 为偶数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第
为偶数,接下来各项都是偶数,一起到某项为1,下面一项为0,以后全部为0.实际上项为1的项是第 项(
项( 成等比数列),故
成等比数列),故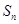 可求;(3)由于
可求;(3)由于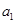 是正整数,要证明从某一项开始,数列各项均为0,这提示我们可首先证明
是正整数,要证明从某一项开始,数列各项均为0,这提示我们可首先证明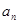 为非负(这可用数学归纳法加以证明),然后由于数列的关系,可见数列在出现0之前,是递减的,下面要考虑的是递减的速度而已.当
为非负(这可用数学归纳法加以证明),然后由于数列的关系,可见数列在出现0之前,是递减的,下面要考虑的是递减的速度而已.当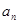 为偶数时,
为偶数时,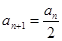 ;当
;当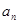 为奇数时,
为奇数时, ,因此对所有正整数
,因此对所有正整数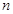 ,都有
,都有 ,依此类推有
,依此类推有 ,只要
,只要 ,则有
,则有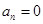 .
.
试题解析:(1)∵ 为偶数,∴可设
为偶数,∴可设 ,故
,故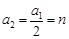 ,
,
若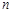 为偶数,则
为偶数,则 ,由
,由 成等差数列,可知
成等差数列,可知 ,
,
即 ,解得
,解得 ,故
,故 ; (2分)
; (2分)
若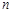 为奇数,则
为奇数,则 ,由
,由 成等差数列,可知
成等差数列,可知 ,
,
即 ,解得
,解得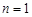 ,故
,故 ;
;
∴ 的值为0或2. (4分)
的值为0或2. (4分)
(2)∵ 是奇数,∴
是奇数,∴ ,
, ,
, ,依此类推,
,依此类推,
可知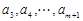 成等比数列,且有
成等比数列,且有
 ,
,
又 ,
, ,
, ,
,
∴当 时,
时, ;当
;当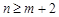 时,都有
时,都有 . (3分)
. (3分)
故对于给定的 ,
, 的最大值为
的最大值为

 ,所以
,所以 . (6分)
. (6分)
(3)当 为正整数时,
为正整数时,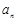 必为非负整数.证明如下:
必为非负整数.证明如下:
当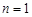 时,由已知
时,由已知 为正整数, 可知
为正整数, 可知 为非负整数,故结论成立;
为非负整数,故结论成立;
假设当 时,
时,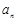 为非负整数,若
为非负整数,若


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
已知点(1,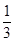 )是函数
)是函数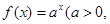 且
且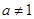 )的图象上一点,等比数列
)的图象上一点,等比数列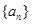 的前
的前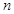 项和为
项和为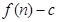 ,数列
,数列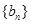
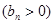 的首项为
的首项为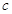 ,且前
,且前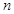 项和
项和 满足
满足 -
-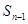 =
=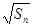 +
+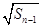 (
( ).
).
(1)求数列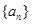 和
和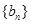 的通项公式;
的通项公式;
(2)求数列{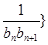 前
前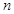 项和为
项和为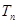 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com