
����Ŀ�����н�������ȷ���ǣ� ��
A.��ֱ�������ε�һ������ֱ��Ϊ��ת�ᣬ���������תһ�ܶ��γɵ�����Χ�ɵļ�������һ��Բ
B.��ֱ�����ε�һ������ֱ��Ϊ��ת�ᣬ���������תһ�ܶ��γɵ�����Χ�ɵļ�������һ��Բ̨
C.��ƽ���ı��ε�һ������ֱ��Ϊ��ת�ᣬ���������תһ�ܶ��γɵ�����Χ�ɵļ�������һ��Բ��
D.Բ������һ��ֱ������ֱ����ת![]() ��õ��ļ�������һ����
��õ��ļ�������һ����
���𰸡�D
��������
Բ����ת����һֱ�DZ����ڵ�ֱ�ߣ�����![]() ����ȷ��Բ̨����ת���Ǵ�ֱ�ױߵ�������ֱ�ߣ�����
����ȷ��Բ̨����ת���Ǵ�ֱ�ױߵ�������ֱ�ߣ�����![]() ����Բ���Ǿ�������ת����ת�����ģ�����
����Բ���Ǿ�������ת����ת�����ģ�����![]() ��������Ķ����жϣ�
��������Ķ����жϣ�![]() ��ȷ.
��ȷ.
��ѡ��A�У�����ֱ�������ε�б������ֱ����תһ�ܣ�
��õ��ļ����岻��һ��Բ����ѡ��A����
��ѡ��B�У�����ֱ�����ε��ϵ�����ֱ����תһ�ܣ�
��õ��ļ����岻��Բ̨����ѡ��B����
��ѡ��C�У���ƽ���ı��ε�һ���ڽ�Ϊ��ǣ�
������һ������ֱ����תһ�ܣ��õ��ļ����岻��Բ����
��ѡ��C����
��ѡ��D�У�Բ������һ��ֱ������ֱ����ת![]() ��õ��ļ�������һ����
��õ��ļ�������һ����
��ѡ��D��ȷ.
��ѡ:D.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P����������O��0��0����A��3��0���ľ���ı�ֵΪ2����P�Ĺ켣Ϊ����C��
��1��������C�Ĺ켣����
��2�����㣨��1��0����ֱ��������C����A��B���㣬���M����Ϊ��4��0�������ABM��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������
��1���ڵȲ�����![]() �У�
��![]() ��
��![]() �ij�Ҫ������
�ij�Ҫ������
��2����֪�ȱ�����![]() Ϊ�������У��ҹ���Ϊ
Ϊ�������У��ҹ���Ϊ![]() ����
����![]() �����ҽ���
�����ҽ���![]() ��
��
��3��������![]() Ϊ�������У���
Ϊ�������У���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��4����֪����![]() ����
����![]() ��������
��������![]() ��ͨ�ʽΪ
��ͨ�ʽΪ![]()
��5����![]() �ǵȱ�����
�ǵȱ�����![]() ��ǰ
��ǰ![]() ��ĺͣ���
��ĺͣ���![]() ��������
��������![]() ��
��![]() �Ƿ��㳣����
�Ƿ��㳣����![]() ������A+BΪ�㣮
������A+BΪ�㣮
������ȷ������_________��ֻ��д����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ABCD�У���E��F�ֱ���AB��BC���е㣬������������ȷ�������______
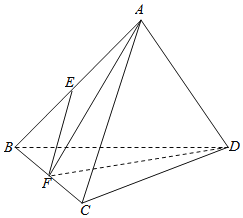
������ֱ��AB��CD���ɽ�Ϊ90����
��ֱ��AB��ƽ��BCD���ɽ�Ϊ60����
��ֱ��EF��ƽ��ACD
��ƽ��AFD��ƽ��BCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1����x��0ʱ��֤��![]() ��
��
��2����x��-1��x��0ʱ������ʽ![]() ���������ʵ��k��ֵ.
���������ʵ��k��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ƴ�һ���������ÿ������ijɱ���Ϊ4Ԫ���ۼ�Ϊ10Ԫ���ÿ��������ֻ��һ¯��һ¯����15��������30�������������û�����꣬ʣ��������ÿ��2Ԫ�ļ۸�������Ϊ��ȷ����һ¯����ĸ������õ��¼�������������30���������������λ���������������±���

��1�����ݱ������ݿ�֪��Ƶ��![]() ����������
����������![]() ����λ������������أ���
����λ������������أ���![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��2����30���¼�ĸ�����������Ƶ�ʴ�������������ĸ��ʣ����õ�����������¯�ĸ���Ϊ24���ǵ�������������õ�������Ϊ![]() ����λ��Ԫ��.
����λ��Ԫ��.
����������������Ϊ15������![]() ��
��
��������![]() �ķֲ��м�����ѧ����.
�ķֲ��м�����ѧ����.
��ع�ʽ��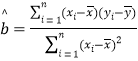
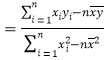 ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��������ʵ��
��������ʵ��![]() ����
����
��1���ֱ����p��q�й���x�IJ���ʽ�Ľ⼯M��N��
��2����p��q�ı�Ҫ�������������ʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() �У��ı���
�У��ı���![]() Ϊ���Σ�
���� ![]() ����������
Ϊ���������Σ� ![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.
���е�.

��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��3��������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ӽס��������˶�Ա��ϰ����ÿ����ϰ10�飬ÿ�鷣��40�������и����ľ�Ҷͼ��ͼ�������������������һ����(����)

A. �ļ�����29 B. ����λ����24
C. ���������ʱ��Ҹ� D. �ҵ�������21
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com