
【题目】设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是________.(填序号)
① 若a⊥b,a⊥α,则b∥α;② 若a∥α,α⊥β,则a⊥β;
③ 若a⊥β,α⊥β,则a∥α;④ 若a⊥b,a⊥α,b⊥β,则α⊥β.
【答案】④
【解析】对于①,根据![]() ,则
,则![]() 或
或![]() ,不一定得出
,不一定得出![]() ,由此可得①不正确;对于②,若a∥α,α⊥β,则可能
,由此可得①不正确;对于②,若a∥α,α⊥β,则可能![]() ,因此②不正确;;对于③,
,因此②不正确;;对于③,![]() ,则
,则![]() 或
或![]() ,不一定得出
,不一定得出![]() ,由此可得③不正确;对于④,由
,由此可得③不正确;对于④,由![]() 且
且![]() ,可得直线
,可得直线![]() 所成角或其补角等于平面
所成角或其补角等于平面![]() 所成角,又因为
所成角,又因为![]() ,可得直线
,可得直线![]() 所成角对于
所成角对于![]() ,由此可得
,由此可得![]() ,所以④是真命题,综上所述,可得正确命题的序号为④,故答案为④.
,所以④是真命题,综上所述,可得正确命题的序号为④,故答案为④.
【方法点晴】本题主要考查线面平行的判定与性质、面面垂直的性质及线面垂直的判定,属于难题.空间直线、平面平行或垂直等位置关系命题的真假判断,常采用画图(尤其是画长方体)、现实实物判断法(如墙角、桌面等)、排除筛选法等;另外,若原命题不太容易判断真假,可以考虑它的逆否命题,判断它的逆否命题真假,原命题与逆否命题等价.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,![]() 轴为正半轴建立极坐标系,圆
轴为正半轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为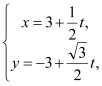 (t为参数).
(t为参数).
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)求直线![]() 分圆
分圆![]() 所得的两弧程度之比.
所得的两弧程度之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
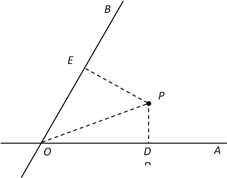
【题目】如图,![]() 、
、![]() 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),![]() ,在
,在![]() 内有一纪念塔
内有一纪念塔![]() (大小忽略不计),已知
(大小忽略不计),已知![]() 到直线
到直线![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,
,![]() =6千米,
=6千米,![]() =12千米.现经过纪念塔
=12千米.现经过纪念塔![]() 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .
.
(1)求纪念塔![]() 到两条公路交点
到两条公路交点![]() 处的距离;
处的距离;
(2)若纪念塔![]() 为小路
为小路![]() 的中点,求小路
的中点,求小路![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中点为D,B1C∩BC1=E. 求证:
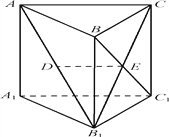
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:![]() .
.
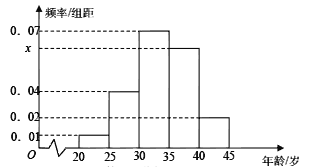
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]()
![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]()
![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]()
![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]()
![]() 时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
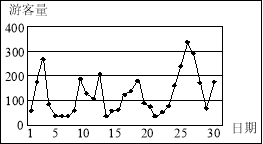
(Ⅰ)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量 (单位:百人) |
|
|
|
|
天数 |
|
|
|
|
频率 |
|
|
|
|
(Ⅱ)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com