
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)求![]() 和平面
和平面![]() 所成的角的大小.
所成的角的大小.
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)推导出![]() .又
.又![]() ,从而
,从而![]() 平面
平面![]() .进而
.进而![]() 为
为![]() 和平面
和平面![]() 所成的角,由此能示出
所成的角,由此能示出![]() 和平面
和平面![]() 所成的角的大小.
所成的角的大小.
(2)推导出![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() 平面
平面![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角.由此能求出二面角
的平面角.由此能求出二面角![]() 的正弦值.
的正弦值.
解:(1)在四棱锥![]() 中,∵
中,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .又
.又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
故![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,从而
,从而![]() 为
为![]() 和平面
和平面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,故
,故![]() .
.
所以![]() 和平面
和平面![]() 所成的角的大小为
所成的角的大小为![]() .
.
(2)在四棱锥![]() 中,∵
中,∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
由条件![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() .由
.由![]() ,
,![]() ,可得
,可得![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .又∵
.又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,如图所示.
,如图所示.
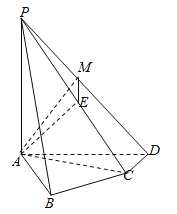
∵![]() 平面
平面![]() ,
,![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,
,
∴![]() .∴
.∴![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知∵![]() ,∴设
,∴设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 中,
中,![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,得
,得![]() .
.
在![]() 中,
中,![]() .
.
所以二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: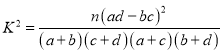
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“杨辉三角”是我国数学史上的一个伟大成就,是二项式系数在三角形中的一种几何排列.如图所示,去除所有为1的项,依此构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前46项和为_____.
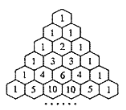
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东![]()
 且与点A相距
且与点A相距![]() 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/时);
(2)若该船不改变航行方向继续行驶判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,g(x)=a
,g(x)=a![]()
(1)当a=3时,解不等式(关于x的)f(x)![]() g(x)+3.
g(x)+3.
(2)若f(x)![]() g(x)-1 对于任意x
g(x)-1 对于任意x![]() 都成立,求a的取值范围。
都成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 幂函数的图象都经过![]() 、
、![]() 两点
两点
B. 当![]() 时,函数
时,函数![]() 的图象是一条直线
的图象是一条直线
C. 如果两个幂函数的图象有三个公共点,那么这两个函数一定相同
D. 如果幂函数为偶函数,则图象一定经过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了100名魔方爱好者进行调查,得到的部分数据如表所示:已知在全部100人中随机抽取1人抽到喜欢盲拧的概率为![]() .
.
喜欢盲拧 | 不喜欢盲拧 | 总计 | |
男 | 10 | ||
女 | 20 | ||
总计 | 100 |
表(1)
并邀请这100人中的喜欢盲拧的人参加盲拧三阶魔方比赛,其完成时间的频率分布如表所示:
完成时间(分钟) | [0,10) | [10,20) | [20,30) | [30,40] |
频率 | 0.2 | 0.4 | 0.3 | 0.1 |
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中完成时间在[30,40] 内的人中任意抽取2人对他们的盲拧情况进行视频记录,记完成时间在[30,40]内的甲、乙、丙3人中恰有一人被抽到为事件A,求事件A发生的概率.
(参考公式: ,其中
,其中![]() )
)
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知直线
轴正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并指出该曲线是什么曲线;
的直角坐标方程,并指出该曲线是什么曲线;
(2)若直线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com