
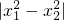 的取值范围为________.
的取值范围为________. |的范围,而|x12-x22|=|(x1+x2)•(x1-x2)|=|
|的范围,而|x12-x22|=|(x1+x2)•(x1-x2)|=| |•|x1-x2|=|
|•|x1-x2|=| |•|1-x2 |,从而可求出
|•|1-x2 |,从而可求出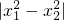 的取值范围.
的取值范围. >-
>- ,0≤|
,0≤| |<1.
|<1. ,x2=
,x2= <0,且对称轴为 x=-
<0,且对称轴为 x=- ∈(-
∈(- ,
, ).
). |•|x1-x2|=|
|•|x1-x2|=| |•|1-x2 |可得,
|•|1-x2 |可得, |=0时,|x12-x22|=|
|=0时,|x12-x22|=| |•|1-x2 |的最小值等于0.
|•|1-x2 |的最小值等于0. )|=2|(1+
)|=2|(1+ )|≤2+|
)|≤2+| |<2+1=3,
|<2+1=3, |•|1-x2 |<1×3=3.
|•|1-x2 |<1×3=3.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com