
【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中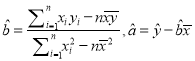
(注: ![]() )
)
【答案】(1)![]() ;(2)12.38
;(2)12.38
【解析】试题分析: ![]() 先把数据列表,由题中所给的数据求出
先把数据列表,由题中所给的数据求出![]() ,
, ![]() ,根据最小二乘法做出线性回归方程的系数
,根据最小二乘法做出线性回归方程的系数![]() ,再根据样本中心点一定在线性回归方程上,求出
,再根据样本中心点一定在线性回归方程上,求出![]() 的值,从而得到线性回归方程;
的值,从而得到线性回归方程; ![]() 由
由![]() 取
取![]() ,计算出对应的
,计算出对应的![]() 的值,即使估计使用年限为
的值,即使估计使用年限为![]() 年时,维修费的估计值
年时,维修费的估计值
解析:(1)先把数据列表如下.
i | 1 | 2 | 3 | 4 | 5 | ∑ |
xi | 2 | 3 | 4 | 5 | 6 | 20 |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | 25 |
xiyi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 | 112.3 |
x | 4 | 9 | 16 | 25 | 36 | 90 |
由表知,![]() =4,
=4,![]() =5,由公式可得:
=5,由公式可得:
![]() =
=![]() =
=![]() =1.23,
=1.23,![]() =
=![]() -
-![]()
![]() =5-1.23×4=0.08,
=5-1.23×4=0.08,
∴回归方程为![]() =1.23x+0.08.
=1.23x+0.08.
(2)由回归方程![]() =1.23x+0.08知,当x=10时,
=1.23x+0.08知,当x=10时,
![]() =1.23×10+0.08=12.38(万元).
=1.23×10+0.08=12.38(万元).
故估计使用年限为10年时维修费用是12.38万元.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1-![]() (a>0,a≠1)且f(0)=0.
(a>0,a≠1)且f(0)=0.
(1)求a的值;
(2)若函数g(x)=(2x+1)·f(x)+k有零点,求实数k的取值范围;
(3)当x∈(0,1)时,f(x)>m·2x-2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线
的直线![]() 交动点
交动点![]() 的轨迹于
的轨迹于![]() 、
、![]() 两点, 且
两点, 且![]() 为线段
为线段![]() ,
,![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把定义域为![]() 且同时满足以下两个条件的函数
且同时满足以下两个条件的函数![]() 称为“
称为“![]() 函数”:(1)对任意的
函数”:(1)对任意的![]() ,总有
,总有![]() ;(2)若
;(2)若![]() ,
,![]() ,则有
,则有![]() 成立,下列判断正确的是( )
成立,下列判断正确的是( )
A.若![]() 为“
为“![]() 函数”,则
函数”,则![]()
B.若![]() 为“
为“![]() 函数”,则
函数”,则![]() 在
在![]() 上为增函数
上为增函数
C.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
D.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求椭圆的方程;
(2)已知过椭圆右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,当天每售出![]() 个利润为
个利润为![]() 元,未售出的每个亏损
元,未售出的每个亏损![]() 元.根据以往
元.根据以往![]() 天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了
天的统计资料,得到如下需求量表,元旦这天,此蛋糕店制作了![]() 个这种蛋糕.以
个这种蛋糕.以![]() (单位:个,
(单位:个, ![]() )表示这天的市场需求量.
)表示这天的市场需求量. ![]() (单位:元)表示这天售出该蛋糕的利润.
(单位:元)表示这天售出该蛋糕的利润.
需求量/个 |
|
|
|
|
|
天数 | 10 | 20 | 30 | 25 | 15 |
(1)将![]() 表示为
表示为![]() 的函数,根据上表,求利润
的函数,根据上表,求利润![]() 不少于
不少于![]() 元的概率;
元的概率;
![]() 天的平均需求量(同一组数据用该区间的中点值作代表);
天的平均需求量(同一组数据用该区间的中点值作代表);
(3)元旦这天,该店通过微信展示打分的方式随机抽取了![]() 名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为
名市民进行问卷调查,调查结果如下表所示,已知在购买意愿强的市民中,女性的占比为![]() .
.
购买意愿强 | 购买意愿弱 | 合计 | |
女性 | 28 | ||
男性 | 22 | ||
合计 | 28 | 22 | 50 |
完善上表,并根据上表,判断是否有![]() 的把握认为市民是否购买这种蛋糕与性别有关?
的把握认为市民是否购买这种蛋糕与性别有关?
附:  .
.
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com