
定义在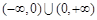 上的函数
上的函数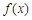 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列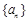 ,
,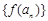 仍是等比数列,则称
仍是等比数列,则称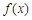 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在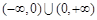 上的如下函数: ①
上的如下函数: ①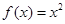 ; ②
; ②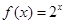 ; ③
; ③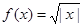 ; ④
; ④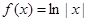 .
.
则其中是“保等比数列函数”的 的序号为
的序号为
A.①② B.③④ C.①③ D.②④
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
(2012年高考(湖北文))定义在![]() 上的函数
上的函数![]() ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列![]() 仍是等比数列,则称
仍是等比数列,则称![]() 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在![]() 上的如下函数:①
上的如下函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则其中是“保等比数列函数”的![]() 的序号为 ( )
的序号为 ( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考(湖北理))定义在![]() 上的函数
上的函数![]() ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列![]() ,
, ![]() 仍
仍
是等比数列,则称![]() 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在![]() 上的如下函
上的如下函
数:①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
则其中是“保等比数列函数”的![]() 的序号为 ( )
的序号为 ( )
A.① ② B.③ ④ C.① ③ D.② ④
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,
,
都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
已知函数![]() ;
; ![]()
(1)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com