
已知椭圆的中心为坐标原点O,焦点在x轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点, 与
与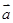 =(3,-1)共线.
=(3,-1)共线.
(1)求椭圆的离心率;
(2)设M为椭圆上任意一点,且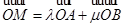 (
(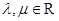 ),证明
),证明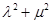 为定值.
为定值.
(1)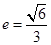 ;(2)
;(2)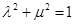
【解析】
试题分析:(1)设椭圆方程为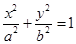 ,直线AB:y=x-c,
,直线AB:y=x-c,
联立消去y可得: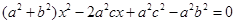 ,
,
令A(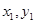 ),B (
),B (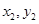 ),
),
则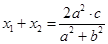 ,
,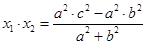 ,
,
向量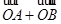 =(
=( ,
, ), 与向量
), 与向量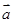 =(3,-1)共线,
=(3,-1)共线,
所以3( )+(
)+( )=0,
)=0,
即3( -2c)+(
-2c)+( )=0,
)=0,
4( )-6c=0,
)-6c=0,
化简得: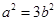 ,
,
所以离心率为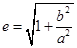 =
=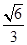 。
。
(2)椭圆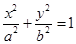 即:
即: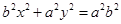 ①
①
设向量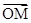 =(x,y),
=(x,y),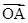 =(
=(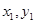 ),
),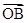 =(
=(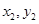 )
)
(x,y)=λ(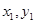 )+μ(
)+μ(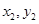 )
)
即:x=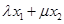 ,y=
,y=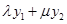
M在椭圆上,把坐标代入椭圆方程① 得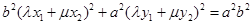 ②
②
直线AB的方程与椭圆方程联立得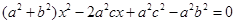 ,由(1)
,由(1)
已证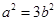 ,所以
,所以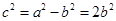
所以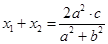 =
= ,
,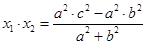 =
=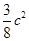 ,
,
而A,B在椭圆上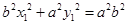 ,
,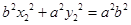
全部代入②整理可得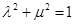 为定值。
为定值。
考点:本题主要考查向量共线的条件,直线与椭圆的位置关系。
点评:典型题,涉及直线与椭圆的位置关系问题,通过联立方程组得到一元二次方程,应用韦达定理可实现整体代换,简化解题过程。


科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a2 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com