
【题目】如图,在三棱柱![]() 中,
中,![]() 和
和![]() 均是边长为2的等边三角形,点
均是边长为2的等边三角形,点![]() 为
为![]() 中点,平面
中点,平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】分析:(1)先根据等腰三角形性质得A1O⊥AC,再根据面面垂直性质定理即得结论,(2)先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解得平面A1BC1的法向量,根据向量数量积得向量夹角,最后根据线面角与向量夹角互余关系求结果.
详解:
(Ⅰ)证明:∵AA1=A1C,且O为AC的中点,
∴A1O⊥AC,
又∵平面AA1C1C⊥平面ABC,且交线为AC,又A1O平面AA1C1C,
∴A1O⊥平面ABC
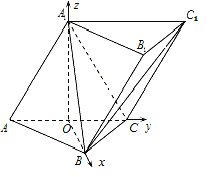
(Ⅱ)如图,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知可得![]() ,
,![]() ,
,![]()
![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设平面A1BC1的法向量为![]()
![]() ,
,
则有![]() ,
,
所以![]() 的一组解为
的一组解为![]()
![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]()
又∵img src="http://thumb.zyjl.cn/questionBank/Upload/2019/02/09/10/12b67617/SYS201902091002258755809350_DA/SYS201902091002258755809350_DA.024.png" width="60" height="33" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ![]() =
= ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】2018年1月26日,甘肃省人民政府办公厅发布《甘肃省关于餐饮业质量安全提升工程的实施意见》,卫生部对16所大学食堂的“进货渠道合格性”和“食品安全”进行量化评估.满10分者为“安全食堂”,评分7分以下的为“待改革食堂”.评分在4分以下考虑为“取缔食堂”,所有大学食堂的评分在7~10分之间,以下表格记录了它们的评分情况:

(1)现从16所大学食堂中随机抽取3个,求至多有1个评分不低于9分的概率;
(2)以这16所大学食堂评分数据估计大学食堂的经营性质,若从全国的大学食堂任选3个,记![]() 表示抽到评分不低于9分的食堂个数,求
表示抽到评分不低于9分的食堂个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
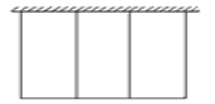
【题目】有一批材料可以建成200m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形,如何设计这块矩形场地的长和宽,能使面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数y=4cos2x-4![]() sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com