
已知椭圆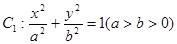 过点
过点 ,且它的离心率
,且它的离心率 .直线
.直线
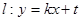 与椭圆
与椭圆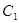 交于
交于 、
、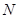 两点.
两点.

(Ⅰ)求椭圆的标准方程;
(Ⅱ)当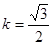 时,求证:
时,求证: 、
、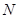 两点的横坐标的平方和为定值;
两点的横坐标的平方和为定值;
(Ⅲ)若直线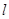 与圆
与圆 相切,椭圆上一点
相切,椭圆上一点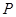 满足
满足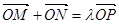 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)  ;
;
(Ⅱ) ,为定值.
,为定值.
(Ⅲ) 的取值范围为
的取值范围为  .
.
【解析】
试题分析:(Ⅰ) 设椭圆的标准方程为
由已知得: ,解得
,解得 
所以椭圆的标准方程为: 4分
4分
(Ⅱ) 由 ,得
,得 ,设
,设 ,
, ,
,
则 ,为定值. 9分
,为定值. 9分
(Ⅲ)因为直线 与圆
与圆 相切
相切
所以,
把 代入
代入 并整理得:
并整理得:
设 ,则有
,则有 

因为, , 所以,
, 所以,
又因为点 在椭圆上, 所以,
在椭圆上, 所以,
 . 因为
. 因为
 所以
所以
 ,
,
所以  ,所以
,所以  的取值范围为
的取值范围为  .
16分
.
16分
考点:本题主要考查椭圆的标准方程,椭圆的几何性质,直线与圆、椭圆的位置关系,二次函数性质。
点评:中档题,涉及椭圆的题目,在近些年高考题中是屡见不鲜,往往涉及求标准方程,研究直线与椭圆的位置关系。求标准方程,主要考虑定义及a,b,c,e的关系,涉及直线于椭圆位置关系问题,往往应用韦达定理。涉及直线于圆的位置关系问题,往往利用“特征三角形”。本题在应用韦达定理的基础上,得到参数的表达式,应用二次函数性质使问题得解。


科目:高中数学 来源:2012-2013学年天津市高三毕业班联考文科数学试卷(解析版) 题型:解答题
已知中心在坐标原点,焦点在 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.

(Ⅰ)求椭圆的标准方程;
(Ⅱ)与圆 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数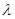 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省绍兴市诸暨中学高二(上)期中数学试卷(文科)(解析版) 题型:解答题
 过点
过点 ,
, ,P(x,y)是椭圆上任一点,O是坐标原点,△PAB椭圆C的内接三角形,且O是△PAB的重心.
,P(x,y)是椭圆上任一点,O是坐标原点,△PAB椭圆C的内接三角形,且O是△PAB的重心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com