
����Ŀ��ij����ƽ̨Ϊ�����������Ч�ʣ������������ҵ������������µ����ͷ�����Ϊ�Ƚ��������ͷ�����Ч�ʣ���ѡȡ50���������֣�������������ֳ����飬ÿ��25�ˣ���һ�������ü����ͷ������ڶ��������������ͷ���.������������ͬʱ����������Ͷ�������������λ���������������¾�Ҷͼ��
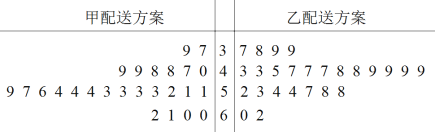
��1�����ݾ�Ҷͼ���������25λ������ɶ���������λ������֪�ü����ͷ�����25λ������ɶ�������ƽ����Ϊ52�������λ����ƽ�����ж��������ͷ�����Ч�ʸ��ߣ���˵�����ɣ�
��2��������50����������ͬʱ������ɶ�������ƽ����![]() ������ɶ���������
������ɶ���������![]() ��Ϊ�����㡱��������
��Ϊ�����㡱��������![]() ��Ϊ��һ�㡱��Ȼ�����ֵĶ�Ӧ��������������������
��Ϊ��һ�㡱��Ȼ�����ֵĶ�Ӧ��������������������
���� | һ�� | |
�����ͷ��� | ||
�����ͷ��� |
��3�����ݣ�2���е����������ж��ܷ���![]() �İ�����Ϊ�������ͷ�����Ч���в���.
�İ�����Ϊ�������ͷ�����Ч���в���.
����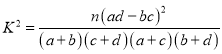 ������
������![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
���𰸡���1������λ��Ϊ53������λ��Ϊ49�������ͷ�����Ч�ʸ��ߣ����������2���������������3����![]() �İ�����Ϊ�������ͷ�����Ч���в���
�İ�����Ϊ�������ͷ�����Ч���в���
��������
��1����Ҷͼ��ȫ��ӳ���е�ԭʼ���ݣ��ɾ�Ҷͼֱ�ӵü���λ��53������λ��49
��2�����ƽ����![]() �ɾ�Ҷͼ����ֱ������
�ɾ�Ҷͼ����ֱ������![]() ��������
��������
��3�����빫ʽ�������![]() ��ֵ��������Լ����жϱ��Ƚ������ж�.
��ֵ��������Լ����жϱ��Ƚ������ж�.
�⣺��1���ü����ͷ��������������������������λ��Ϊ53��
�������ͷ��������������������������λ��Ϊ49��
��Ϊ�������ͷ������������������������ƽ����Ϊ![]() ��
��![]() ��
��
���ԣ������ͷ�����Ч�ʸ���.
��2���ɾ�Ҷͼ֪![]() .
.
���������£�
���� | һ�� | |
�����ͷ��� | 17 | 8 |
�����ͷ��� | 9 | 16 |
��3����Ϊ![]() ��
��
������![]() �İ�����Ϊ�������ͷ�����Ч���в���.
�İ�����Ϊ�������ͷ�����Ч���в���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����������
����������![]() �ɵȲ����Ϊ
�ɵȲ����Ϊ![]() ��ż����
��ż����![]() �ɵȱȣ�����Ϊ
�ɵȱȣ�����Ϊ![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��
��![]() ��
��![]() .
.
![]() ��
��![]() ��
��![]() .
.
��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
����![]() ����������
����������![]() ��ֵ��
��ֵ��
![]() ��
��![]() ��
��![]() �������������
�������������![]() ���Ƿ����ʵ��
���Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ������������ڣ����
������������ڣ����![]() ��ȡֵ��Χ���������ڣ���˵������.
��ȡֵ��Χ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2����֪ʵ��![]() ʱ����֤������
ʱ����֤������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ��
��![]() ��3�����㣮
��3�����㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ�ļƻ�����ģ�ͣ�ÿ����ͥ�������к����һ������ijһ̥��Ϊ�к�������������һ̥����Ů�����Զ��.Ϊ����������˴�Լ��ÿ����ͥ��������3��С����������һ̥��ǰ��̥ΪŮ���������������������̥����Ů��������������.��ÿһ̥������Ů�ȿ��ܣ��Ҹ������������.����ÿ����ͥ�������һ���к��������Լ����Ƕ�����Ů����Լ������![]() Ϊijһ��ͥ������Ů������
Ϊijһ��ͥ������Ů������![]() Ϊ�˼�ͥ�������к���.
Ϊ�˼�ͥ�������к���.
��1����![]() ��
��![]() �ķֲ��У����Ƚ�������ѧ�����Ĵ�С��
�ķֲ��У����Ƚ�������ѧ�����Ĵ�С��
��2�������![]() ������
������![]() Ϊ
Ϊ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽��˶��������ʵ�Ч����ij������������20�������ߣ�����֮ǰ���ǵ�����(��λ��![]() )���������ͼ1��ʾ�������ĸ��µĽ��������ǵ��������������ͼ2��ʾ.�ԱȽ���ǰ������20�������ߣ����������ȷ���ǣ� ��
)���������ͼ1��ʾ�������ĸ��µĽ��������ǵ��������������ͼ2��ʾ.�ԱȽ���ǰ������20�������ߣ����������ȷ���ǣ� ��
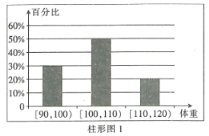
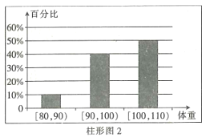
A.���ǽ���������������![]() �ڵ�����������2��
�ڵ�����������2��
B.���ǽ���������������![]() �ڵ�����û�иı�
�ڵ�����û�иı�
C.��Ϊ������![]() ����ռ����û�з����仯������˵������������û���κ�Ӱ��
����ռ����û�з����仯������˵������������û���κ�Ӱ��
D.���ǽ�����ԭ������������![]() �ڵķ��������ض��м���
�ڵķ��������ض��м���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1������![]() �ļ�ֵ��ĸ�����
�ļ�ֵ��ĸ�����
��2���躯��![]() ��
��![]() ��
��![]() ����
Ϊ����![]() ������������ͬ�ĵ㣬��ֱ��
������������ͬ�ĵ㣬��ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��A1B1C1D1�У�M��N��P�ֱ���C1D1��BC��A1D1���е㣬�������ĸ����ۣ�
��AP��CM������ֱ�ߣ���AP��CM��DD1�ཻ��һ�㣻��MN��BD1��
��MN��ƽ��BB1D1D��
����������ȷ���۵ı���ǣ�������

A.�٢�B.�ڢ�C.�٢�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊƽ����һ�㣬
Ϊƽ����һ�㣬![]() Ϊֱ��
Ϊֱ��![]() ��
��![]() ������һ�㣬����
������һ�㣬����![]() ��ֱ��
��ֱ��![]() �Ĵ���
�Ĵ���![]() �����߶�
�����߶�![]() ���д�����ֱ��
���д�����ֱ��![]() ���ڵ�
���ڵ�![]() ���ǵ�
���ǵ�![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
��1����켣![]() �ķ��̣�
�ķ��̣�
��2������![]() �����ഹֱ��ֱ��
�����ഹֱ��ֱ��![]() ��
��![]() ������ֱ��
������ֱ��![]() ��켣
��켣![]() ���ڵ�
���ڵ�![]() ��
��![]() ��ֱ��
��ֱ��![]() ��켣
��켣![]() ���ڵ�
���ڵ�![]() ��
��![]() �����
�����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬��
���е㣬��![]() ���������Сֵ.
���������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������У���ģ����������������°������£����ﰮ�����徫������������У�����ʦ�齨��һ����Ⱥ��Ⱥ�ij�Ա��ѧ�����ҳ�����ʦ�ͽ���Ա��ͬ���.��֪����Ⱥ����ѧ����������Ů��������Ůѧ���������ڼҳ��������ҳ��������ڽ�ʦ��������ʦ�������ڽ���Ա����������Ա����������������������.������5����Ⱥ��������Ϊһ�����ݣ�������Ⱥ������ȡ��Сֵʱ���������ݵ���λ���ǣ� ��
A.5B.6C.7D.8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com