
【题目】已知实数![]() ,设函数
,设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)对任意![]() 均有
均有![]() 求
求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可.
(2)由题意首先由函数在特殊点的函数值得到a的取值范围,然后证明所得的范围满足题意即可.
(1)当![]() 时,
时,![]() ,函数的定义域为
,函数的定义域为![]() ,且:
,且:
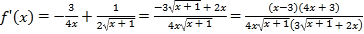 ,
,
因此函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)构造函数![]() ,
,
注意到:![]() ,
,
注意到![]() 时
时![]() 恒成立,满足
恒成立,满足![]() ;
;
当![]() 时,
时,![]() ,不合题意,
,不合题意,
且![]() ,解得:
,解得:![]() ,故
,故![]() .
.
下面证明![]() 刚好是满足题意的实数a的取值范围.
刚好是满足题意的实数a的取值范围.
分类讨论:
(a)当![]() 时,
时,![]() ,
,
令![]() ,则:
,则:
![]()
![]()
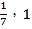
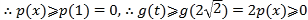 ,
,
易知![]() ,则函数
,则函数![]() 单调递减,
单调递减,![]() ,满足题意.
,满足题意.
(b)当![]() 时,
时,![]() 等价于
等价于![]() ,
,
左侧是关于a的开口向下的二次函数![]() ,
,
其判别式![]() ,
,
令![]() ,注意到当
,注意到当![]() 时,
时,![]() ,
,
于是![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
于是当![]() 时命题成立,
时命题成立,
而当![]() 时,此时
时,此时![]() 的对称轴为
的对称轴为![]() 随着
随着![]() 递增,
递增,
于是对称轴在![]() 的右侧,而
的右侧,而![]() 成立,(不等式等价于
成立,(不等式等价于![]() ).
).
因此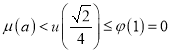 .
.
综上可得:实数a的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】武汉又称江城,是湖北省省会城市,被誉为中部地区中心城市,它不仅有着深厚的历史积淀与丰富的民俗文化,更有着众多名胜古迹与旅游景点,每年来武汉参观旅游的人数不胜数,其中黄鹤楼与东湖被称为两张名片为合理配置旅游资源,现对已游览黄鹤楼景点的游客进行随机问卷调查,若不游玩东湖记1分,若继续游玩东湖记2分,每位游客选择是否游览东湖景点的概率均为![]() ,游客之间选择意愿相互独立.
,游客之间选择意愿相互独立.
(1)从游客中随机抽取3人,记总得分为随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(2)(i)若从游客中随机抽取![]() 人,记总分恰为
人,记总分恰为![]() 分的概率为
分的概率为![]() ,求数列
,求数列![]() 的前10项和;
的前10项和;
(ⅱ)在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为![]() 分的概率为
分的概率为![]() ,探讨
,探讨![]() 与
与![]() 之间的关系,并求数列
之间的关系,并求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由
年以来精准扶贫政策的落实,使我国扶贫工作有了新进展,贫困发生率由![]() 年底的
年底的![]() 下降到
下降到![]() 年底的
年底的![]() ,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,
,创造了人类减贫史上的的中国奇迹.“贫困发生率”是指低于贫困线的人口占全体人口的比例,![]() 年至
年至![]() 年我国贫困发生率的数据如下表:
年我国贫困发生率的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的![]() 个贫困发生率数据中任选两个,求两个都低于
个贫困发生率数据中任选两个,求两个都低于![]() 的概率;
的概率;
(2)设年份代码![]() ,利用线性回归方程,分析
,利用线性回归方程,分析![]() 年至
年至![]() 年贫困发生率
年贫困发生率![]() 与年份代码
与年份代码![]() 的相关情况,并预测
的相关情况,并预测![]() 年贫困发生率.
年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
 (
(![]() 的值保留到小数点后三位)
的值保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金、专业二等奖学金及专业三等奖学金,且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
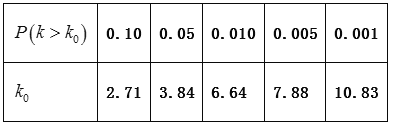
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
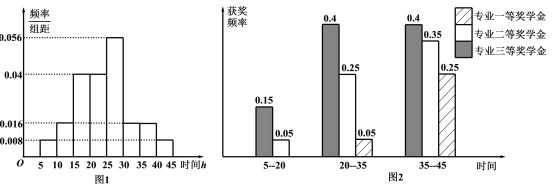
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
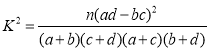
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,且函数
平行,且函数![]() 有两个零点.
有两个零点.
(1)求实数![]() 的值和实数
的值和实数![]() 的取值范围;
的取值范围;
(2)记函数![]() 的两个零点为
的两个零点为![]() ,求证:
,求证: ![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到两定点M(﹣3,0),N(3,0)的距离满足|PM|=2|PN|.
(1)求证:点P的轨迹为圆;
(2)记(1)中轨迹为⊙C,过定点(0,1)的直线l与⊙C交于A,B两点,求△ABC面积的最大值,并求此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com