
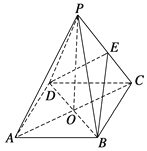
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
【答案】(1)见解析(2)![]() a3
a3
【解析】试题分析:(1) 设法证明平面![]() 内的一条直线
内的一条直线![]() 垂直于平面
垂直于平面![]() 内的两条相交直线即可;(2)取
内的两条相交直线即可;(2)取![]() 中点
中点![]() ,连结
,连结![]() ,由已知条件推导出
,由已知条件推导出![]() 为二面角
为二面角![]() 的平面角,由此能求出四棱锥
的平面角,由此能求出四棱锥![]() 的体积
的体积
试题解析:(1)证明 连接OE,如图所示.
∵PO⊥面ABCD,∴PO⊥BD.在正方形ABCD中,BD⊥AC,
又∵PO∩AC=0,∴BD⊥面PAC.
又∵BD面BDE,∴面PAC⊥面BDE.
(2)
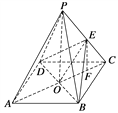 解 取OC中点F,连接EF.
解 取OC中点F,连接EF.
∵E为PC中点,
∴EF为△POC的中位线,∴EF∥PO.
又∵PO⊥面ABCD,
∴EF⊥面ABCD
∵OF⊥BD,∴OE⊥BD.
∴∠EOF为二面角E-BD-C的平面角,
∴∠EOF=30°.
在Rt△OEF中,OF=![]() OC=
OC=![]() AC=
AC=![]() a,∴EF=OF·tan 30°=
a,∴EF=OF·tan 30°=![]() a,∴OP=2EF=
a,∴OP=2EF=![]() a.
a.
∴VP-ABCD=![]() ×a2×
×a2×![]() a=
a=![]() a3.
a3.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 轴上的点.
轴上的点.
(1)过点![]() 作直线
作直线![]() 与
与![]() 相切,求切线
相切,求切线![]() 的方程;
的方程;
(2)如果存在过点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与
与![]() 的倾斜角互补,求实数
的倾斜角互补,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() ,
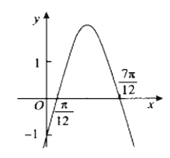
,![]() 的部分图象如图所示,有下列结论:
的部分图象如图所示,有下列结论:
①函数![]() 的最小正周期为
的最小正周期为![]()
②函数![]() 在
在![]() 上的值域为
上的值域为![]()
③函数![]() 的一条对称轴是
的一条对称轴是![]()
④函数![]() 的图象关于点
的图象关于点![]() 对称
对称
⑤函数![]() 在
在![]() 上为减函数
上为减函数
其中正确的是______.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() (
(![]() ,
,![]() ).
).
(1)求函数![]() 的零点;
的零点;
(2)设![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() 为最简根式,若存在
为最简根式,若存在![]() ,使得
,使得![]() 可唯一表示为
可唯一表示为![]() 的形式(
的形式(![]() ),求证:
),求证:![]() ;
;
(3)已知![]() ,是否存在
,是否存在![]() ,使得
,使得![]()
成立,若存在,试求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆O:![]() 与坐标轴分别交于A1,A2,B1,B2(如图).
与坐标轴分别交于A1,A2,B1,B2(如图).
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线![]() 交于不同的两点M,N,求线段MN长的最小值;
交于不同的两点M,N,求线段MN长的最小值;
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设A2P的斜率为k,EF的斜率为m,求证:2m﹣k为定值.
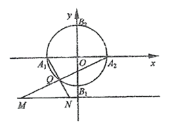
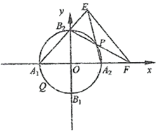
(图1) (图2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,D,E分别为BC,PD的中点,F为AB上一点,且
,D,E分别为BC,PD的中点,F为AB上一点,且![]() .
.
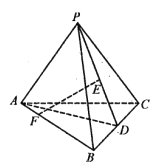
(1)求证:![]() 平面PAD;
平面PAD;
(2)求证:![]() 平面PAC;
平面PAC;
(3)若二面角![]() 为60°,求三棱锥
为60°,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求实数
,求实数![]() 的值;
的值;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时
面积的最大时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com