
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的面积为
的面积为![]() .
.
(1)求该椭圆的标准方程;
(2)过该椭圆的左顶点![]() 作两条相互垂直的直线分别与椭圆相交于不同于点
作两条相互垂直的直线分别与椭圆相交于不同于点![]() 的两点
的两点![]() 、
、![]() ,证明:动直线
,证明:动直线![]() 恒过
恒过![]() 轴上一定点.
轴上一定点.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)由三角形的面积可得![]() .结合椭圆的定义可得
.结合椭圆的定义可得![]() ,则
,则![]() .
.![]() .所求方程为
.所求方程为![]() .
.
(2)假设结论成立,定点坐标设为![]() ,显然
,显然![]() .当直线
.当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的斜率为
的斜率为![]() ,
,![]() 的方程为
的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .当直线
.当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,与椭圆方程联立有
,与椭圆方程联立有![]()
![]() ,
,![]() ,则
,则![]() ,据此可得
,据此可得![]() 或
或![]() ,则直线
,则直线![]() 恒过点
恒过点![]() .详解:(1)∵点
.详解:(1)∵点![]() 在椭圆上,且
在椭圆上,且![]() 的面积为
的面积为![]() ,
,
∴![]() ,即
,即![]() .
.
∴两个焦点坐标分别为![]() 、
、![]() .
.
∴![]() ,即:
,即:![]() .
.
∴![]() .
.
∴所求方程为![]() .
.
(2)假设结论成立,定点坐标设为![]() ,显然
,显然![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴,此时直线
轴,此时直线![]() 的斜率为
的斜率为![]() ,
,
∴![]() 的方程为
的方程为![]() ,代入
,代入![]() 化简得:
化简得:![]() ,
,
∴![]() 或
或![]() ,即此时直线
,即此时直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
当直线![]() 的斜率存在时,设为
的斜率存在时,设为![]() ,依题意,
,依题意,![]() .
.
则![]() 的方程为
的方程为![]() ,
,
代入![]() 并化简得:
并化简得: ![]()
![]() ,
,
设![]() 、
、![]() ,
,
∴![]() ,
,![]() .
.
又![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]() ,解之得
,解之得![]() 或
或![]() ,
,
即直线![]() 恒过点
恒过点![]() .
.
综上所述,直线![]() 恒过定点
恒过定点![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
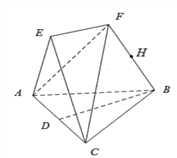
【题目】如图,在三棱锥![]() 与三棱锥
与三棱锥![]() 中,
中,![]() 和
和![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,
,![]() .
.
(Ⅰ)试在平面![]() 内作一条直线
内作一条直线![]() ,当
,当![]() 时,均有
时,均有![]() 平面
平面![]() (作出直线
(作出直线![]() 并证明);
并证明);
(Ⅱ)求两棱锥体积之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 及函数
及函数![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)证明:f(x)的图像与g(x)的图像一定有两个交点;
(2)请用反证法证明:![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市疾控中心流感监测结果显示,自![]() 年
年![]() 月起,该市流感活动一度出现上升趋势,尤其是
月起,该市流感活动一度出现上升趋势,尤其是![]() 月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知
月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知![]() 位同学中有
位同学中有![]() 位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
方案乙:先任取![]() 个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这
个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这![]() 位中的
位中的![]() 位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外
位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外![]() 位同学中逐个检测;
位同学中逐个检测;
(1)求依方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)![]() 表示依方案甲所需化验次数,
表示依方案甲所需化验次数,![]() 表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com