
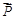 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
= (Ⅰ)求角B的大小;(Ⅱ)设
(Ⅰ)求角B的大小;(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值. .(Ⅱ)k=
.(Ⅱ)k=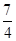 .
. =
= |,两边平方得
|,两边平方得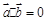 ,……2分
,……2分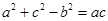 ,……4分
,……4分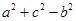 =2 a cosB,所以cosB=
=2 a cosB,所以cosB= ,B=
,B= .……6分
.……6分 =(sin(C+
=(sin(C+ ),
), ),
), =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1), =2ksin(C+
=2ksin(C+ )+
)+ cos2A=2ksin(C+B)+
cos2A=2ksin(C+B)+ cos2A=2ksinA+
cos2A=2ksinA+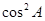 -
-
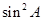 +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).……8分
(k>1).……8分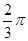 ,sinA∈(0,1],故当sinA=1时,
,sinA∈(0,1],故当sinA=1时, 取最大值为2k-
取最大值为2k- =3,得k=
=3,得k=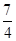 .……12分
.……12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com