
【题目】如图,在长方体![]() 中,
中,![]() 、
、![]() 分别是棱
分别是棱![]() ,
,![]()
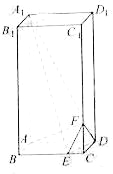
上的点,![]() ,
,![]()
(1) 求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2) 证明![]()
![]() 平面
平面![]()
![]()
(3) 求二面角![]() 的正弦值.
的正弦值.
【答案】(1)![]() ,(2)见解析(3)
,(2)见解析(3)![]()
【解析】
方法一:如图所示,建立空间直角坐标系,
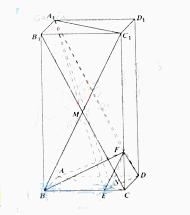
点A为坐标原点,设![]() ,依题意得
,依题意得![]() ,
,
![]() ,
,![]() ,
,![]()
(1) 解:易得![]() ,
,![]()
于是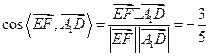
所以异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]()
(2) 证明:已知![]() ,
,![]() ,
,![]()
于是![]() ·
·![]() =0,
=0,![]() ·
·![]() =0.因此,
=0.因此,![]() ,
,![]() ,又
,又![]()
所以![]() 平面
平面![]()
(3)解:设平面![]() 的法向量
的法向量![]() ,则
,则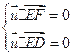 ,即
,即
不妨令X=1,可得![]() .由(2)可知,
.由(2)可知,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
于是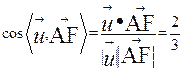 ,从而
,从而![]()
所以二面角![]() 的正弦值为
的正弦值为![]()
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=![]()
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由![]() ,可知EF∥BC1.故
,可知EF∥BC1.故![]() 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=![]() ,所以
,所以![]() ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为![]()
(2)证明:连接AC,设AC与DE交点N 因为![]() ,所以
,所以![]() ,从而
,从而![]() ,又由于
,又由于![]() ,所以
,所以![]() ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且![]() ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为![]() ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF![]() 平面ACF, A1N
平面ACF, A1N![]() 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故![]() 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角
易知![]() ,所以
,所以![]() ,又
,又![]() 所以
所以![]() ,在
,在![]()
![]()
连接A1C1,A1F 在![]()
![]() .所以
.所以![]()
所以二面角A1-DE-F正弦值为![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .斜率为k的直线l与椭圆M有两个不同的交点A,B.
.斜率为k的直线l与椭圆M有两个不同的交点A,B.
(Ⅰ)求椭圆M的方程;
(Ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点
,直线PA与椭圆M的另一个交点为C,直线PB与椭圆M的另一个交点为D.若C,D和点![]() 共线,求k.
共线,求k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬天的北方室外温度极低,若轻薄保暖的石墨烯发热膜能用在衣服上,可爱的医务工作者行动会更方便.石墨烯发热膜的制作:从石墨中分离出石墨烯,制成石墨烯发热膜.从石墨分离石墨烯的一种方法是化学气相沉积法,使石墨升华后附着在材料上再结晶.现在有![]() 材料、
材料、![]() 材料供选择,研究人员对附着在
材料供选择,研究人员对附着在![]() 材料、
材料、![]() 材料上再结晶各做了50次试验,得到如下等高条形图.
材料上再结晶各做了50次试验,得到如下等高条形图.
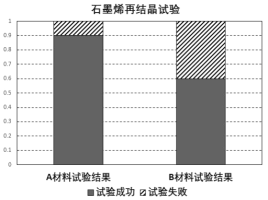
(1)根据上面的等高条形图,填写如下列联表,判断是否有99%的把握认为试验成功与材料有关?
|
| 合计 | |
成功 | |||
不成功 | |||
合计 |
(2)研究人员得到石墨烯后,再制作石墨烯发热膜有三个环节:①透明基底及![]() 胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为
胶层;②石墨烯层;③表面封装层.第一、二环节生产合格的概率均为![]() ,第三个环节生产合格的概率为
,第三个环节生产合格的概率为![]() ,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
,且各生产环节相互独立.已知生产1吨的石墨烯发热膜的固定成本为1万元,若生产不合格还需进行修复,第三个环节的修复费用为3000元,其余环节修复费用均为1000元.如何定价,才能实现每生产1吨石墨烯发热膜获利可达1万元以上的目标?
附:参考公式: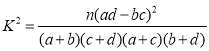 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系中,以原点为极点,以![]() 轴非负半轴为极轴建立极坐标系, 已知曲线
轴非负半轴为极轴建立极坐标系, 已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右顶点,
的左右顶点,![]() 点为椭圆
点为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() .
.
(1)若椭圆![]() 经过圆
经过圆![]() 的圆心,求椭圆
的圆心,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的
相交于不同的![]() 两点,设
两点,设![]() 为椭圆
为椭圆![]() 上一点,且满足
上一点,且满足![]() (
(![]() 为坐标原点),当
为坐标原点),当![]() 时,求实数
时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com