
【题目】如图1,矩形![]() 中,
中, ![]() ,将
,将![]() 沿
沿![]() 折起,得到如图
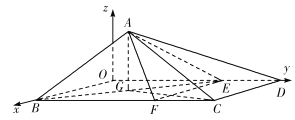
折起,得到如图![]() 所示的四棱锥
所示的四棱锥![]() ,其中
,其中![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
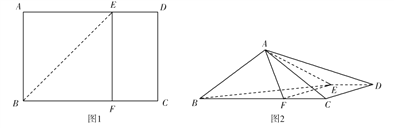
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .易知,
.易知, ![]() ,又求得
,又求得![]() ,
, ![]() ,所以
,所以![]() ,得
,得![]() 所以
所以![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,求得平面![]() 的法向量
的法向量![]() .平面
.平面![]() 的法向量
的法向量
![]() ,所以求得二面角的余弦值为
,所以求得二面角的余弦值为![]() 。
。
试题解析:
(1)在图2中取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() .由条件可知图1中四边形
.由条件可知图1中四边形![]() 为正方形,则有
为正方形,则有![]() ,且可求得
,且可求得![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,由余弦定理得
,由余弦定理得![]() .
.
在![]() 中,
中, ![]() ,所以
,所以![]() ,即
,即![]() .
.
由于![]() ,
, ![]() 平面
平面![]() ,
, ![]() 且
且![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)如图,以![]() 为坐标原点,以平行于
为坐标原点,以平行于![]() 的方向为
的方向为![]() 轴,平行于
轴,平行于![]() 的方向为
的方向为![]() 轴,建立空间直角坐标系.由题设条件,可得
轴,建立空间直角坐标系.由题设条件,可得![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
由(1)得![]() 平面
平面![]() ,可求得
,可求得![]() 点坐标为
点坐标为![]() ,
,
所以![]() ,
, ![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 及
及![]() 得
得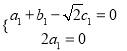 令
令![]() ,由此可得
,由此可得![]() .
.
由于![]() ,
, ![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 及
及![]() 得
得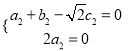 令
令![]() ,由此可得
,由此可得![]()
所以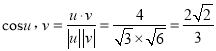
则平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
年级名次 | 1~50 | 951~1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
附:P(K2≥3.841=0.05)K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期为π,且f(
<φ<0)的最小正周期为π,且f( ![]() )=
)= ![]() .
.
(1)求ω和φ的值;
(2)求f(x)的单调递增区间;
(3)求f(x)在[0, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3﹣6x2+1,若f(x)存在唯一的零点x0 , 且x0>0,则a的取值范围是( )
A.(﹣∞,﹣4)
B.(4,+∞)
C.(﹣∞,﹣4 ![]() )
)
D.(4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|y= ![]() },B={x|log2x≤1},则A∩B=( )
},B={x|log2x≤1},则A∩B=( )
A.{x|﹣3≤x≤1}
B.{x|0<x≤1}
C.{x|﹣3≤x≤2}
D.{x|x≤2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com