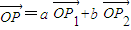练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ（不包括边界）．若，且点P落在第Ⅲ部分，则实数a、b满足（ ）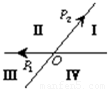

    A．a＞0，b＞0
    B．a＞0，b＜0
    C．a＜0，b＞0
    D．a＜0，b＜0
    【答案】分析：根据所给的图形知，点P落在第Ⅲ部分，则根据实数与向量的积的定义及平行四边形法则知a与方向相同，b与方向相反，得到a与b的符号．
    解答：解：∵=a+b，
    由于点P落在第Ⅲ部分，
    则根据实数与向量的积的定义及平行四边形法则知a与方向相同，
    b与方向相反，
    ∴a＞0，b＜0．
    故选：B．
    点评：本题考查向量的数乘运算，考查向量的加法运算，是一个基础题，但是本题的题意比较新颖，是一个有创新意识的问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：四川省成都外国语学校2012届高三12月月考数学试题 题型：013

    如图：l1，l2，l3，l4是同一平面内的四条平行直线，且每相领的两条平行直线间的距离都是h，正方形ABCD的四个顶点分别在这四条直线上，

    且正方形的边长为5，则h＝

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源：四川省成都外国语学校2012届高三第三次月考数学试题 题型：013

    如图：l1，l2，l3，l4是同一平面内的四条平行直线，且每相领的两条平行直线间的距离都是h，正方形ABCD的四个顶点分别在这四条直线上，且正方形的边长为5，则h＝

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（湖南卷解析版） 题型：解答题

    如图6，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是等腰梯形，AD∥BC，AC⊥BD.

    （Ⅰ）证明：BD⊥PC；

    （Ⅱ）若AD=4，BC=2，直线PD与平面PAC所成的角为30°，求四棱锥P-ABCD的体积.

    【解析】（Ⅰ）因为

    又是平面PAC内的两条相较直线，所以BD平面PAC，

    而平面PAC，所以.

    （Ⅱ）设AC和BD相交于点O，连接PO，由（Ⅰ）知，BD平面PAC，

    所以是直线PD和平面PAC所成的角，从而.

    由BD平面PAC，平面PAC，知.在中，由，得PD=2OD.因为四边形ABCD为等腰梯形，，所以均为等腰直角三角形，从而梯形ABCD的高为于是梯形ABCD面积

    在等腰三角形ＡＯＤ中，

    所以

    故四棱锥的体积为.

    【点评】本题考查空间直线垂直关系的证明，考查空间角的应用，及几何体体积计算.第一问只要证明BD平面PAC即可，第二问由（Ⅰ）知，BD平面PAC，所以是直线PD和平面PAC所成的角，然后算出梯形的面积和棱锥的高，由算得体积

     

    查看答案和解析>>

    科目：高中数学 来源：四川省月考题 题型：单选题

    如图：l1，l2，l3，l4是同一平面内的四条平行直线，且每相领的两条平行直线间的距离都是h，正方形ABCD的四个顶点分别在这四条直线上，且正方形的边长为5，则h=

    [     ]

    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案