
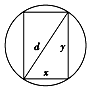
 如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )
如图,横梁的横断面是一个矩形,而横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的高和宽分别为( )| A. | $\sqrt{3}$d,$\frac{\sqrt{3}}{3}$d | B. | $\frac{\sqrt{3}}{3}$d,$\frac{\sqrt{6}}{3}$d | C. | $\frac{\sqrt{6}}{3}$d,$\frac{\sqrt{3}}{3}$d | D. | $\frac{\sqrt{6}}{3}$d,$\sqrt{3}$d |
分析 根据横梁的强度和它的矩形横断面的宽与高的平方的乘积成正比,建立关系.由勾股定理可得x2+y2=d2,利用导函数的性质求出最值.
解答 解:由题意,设横梁的强度为T,则T=xy2.(x>0,y>0)
由勾股定理可得x2+y2=d2,
可得:T=x(d2-x2)=xd2-x3.
则T′=d2-3x2.
令T′=0.
可得:x=$\frac{d}{\sqrt{3}}$或$-\frac{d}{\sqrt{3}}$(舍去).
当$0<x<\frac{d}{\sqrt{3}}$时,可得T′>0,则T是单调递增函数.
当$x>\frac{d}{\sqrt{3}}$时,可得T′<0,则T是单调递减函数.
∴x=$\frac{d}{\sqrt{3}}$时,T取得最大值,此时y=$\sqrt{{d}^{2}-{x}^{2}}$=$\frac{\sqrt{6}}{3}d$.
故选:B.
点评 本题考查了函数模型在实际问题中的应用,利用到了导函数的性质求解最值,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | a | B. | 2a | C. | 2$\sqrt{1-a}$-4 | D. | 2$\sqrt{2-a}$-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2y2-4y-4=0可化为(y-1)2=4 | B. | x2-2x-9=0可化为(x-1)2=8 | ||
| C. | x2+8x-9=0可化为(x+4)2=16 | D. | x2-4x=0可化为(x-2)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 证明n=0时,n2<2n | B. | 证明n=5时,n2<2n | C. | 证明n=1时,n2<2n | D. | 证明n=6时,n2<2n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,3-2\sqrt{2})$ | B. | $(-∞,3+2\sqrt{2})$ | C. | $(3-2\sqrt{2},+∞)$ | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com