Question

直线y=x+2截抛物线y=4-x²所得封闭图形的面积是______．

Answer 1

【答案】分析：先把直线与抛物线的图象画在同一个坐标系中，找出围成封闭图形，然后把直线与抛物线解析式联立求出直线与抛物线的交点坐标，根据图形得到抛物线解析式减去直线解析式在-2到1上的定积分即为阴影图形的面积，求出定积分的值即为所求的面积．
解答：解：根据题意画出图形，如图所示：
联立直线与抛物线解析式得：，
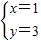
解得：或 ，
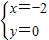
设直线y=x+2截抛物线y=4-x²所得封闭图形的面积为S，
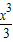
则S=∫_-2¹[（4-x²）-（x+2）]dx=（--+2x）|_-2¹=．
故答案为：．
点评：此题考查了定积分的运算，考查了数形结合的思想，利用定积分表示封闭图形的面积是解本题的关键，属于中档题．