
【题目】已知函数![]() .
.
(1)若![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若存在唯一整数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)本问考查利用导数研究函数单调性,由函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,采用参变分离的方法,将问题转化为
上恒成立,采用参变分离的方法,将问题转化为![]() 在
在![]() 上恒成立,设函数
上恒成立,设函数![]() ,于是只需满足
,于是只需满足![]() 即可,问题转化为求函数
即可,问题转化为求函数![]() 的最小值;(2)存在唯一整数
的最小值;(2)存在唯一整数![]() ,使得
,使得![]() ,即
,即![]() ,于是问题转化为存在唯一一个整数
,于是问题转化为存在唯一一个整数 ![]() 使得函数
使得函数![]() 图像在直线
图像在直线![]() 下方,于是可以画出两个函数图像,结合图像进行分析,确定函数在
下方,于是可以画出两个函数图像,结合图像进行分析,确定函数在![]() 时图像之间的关系,通过比较斜率大小来确定
时图像之间的关系,通过比较斜率大小来确定![]() 的取值范围.
的取值范围.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
要使![]() 在区间
在区间![]() 上单调递增,只需
上单调递增,只需![]() ,即
,即
![]() 在
在![]() 上恒成立即可,
上恒成立即可,
易知![]() 在
在![]() 上单调递增,所以只需
上单调递增,所以只需![]() 即可,
即可,
易知当![]() 时,
时, ![]() 取最小值,
取最小值, ![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.
(2)不等式![]() 即
即![]() ,
,
令![]() ,
,
则![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,
,
∴存在实数![]() ,使得
,使得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() .
.
![]() ,画出函数
,画出函数![]() 和
和![]() 的大致图象如下,
的大致图象如下,
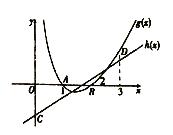
![]() 的图象是过定点
的图象是过定点![]() 的直线,
的直线,
由图可知若存在唯一整数![]() ,使得
,使得![]() 成立,则需
成立,则需![]() ,
,
而![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
于是实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
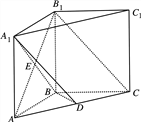
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示. 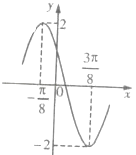
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)求函数f(x)在[﹣ ![]() ,
, ![]() ]上的单调减区间.
]上的单调减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 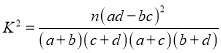 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,且离心率为
,且离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值以及此时直线
面积的最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com