
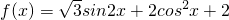 .
. ,△ABC的面积为
,△ABC的面积为 ,求f(A)及a的值.
,求f(A)及a的值. sin2x+2cos2x+2
sin2x+2cos2x+2 sin2x+cos2x+3
sin2x+cos2x+3 sin2x+
sin2x+ cos2x)+3
cos2x)+3 sin2x+sin
sin2x+sin cos2x)
cos2x) )+3…(4分)
)+3…(4分) ,k∈Z时,f(x)有最大值5;
,k∈Z时,f(x)有最大值5; ,k∈Z时,f(x)有最小值1; …(7分)
,k∈Z时,f(x)有最小值1; …(7分) )+3,…(9分)
)+3,…(9分) )=2sin(2×
)=2sin(2× +
+ )+3=2sin
)+3=2sin +3=4…(11分)
+3=4…(11分) bcsinA,则
bcsinA,则 =
= bcsin
bcsin ,
, ,
, …(13分)
…(13分) sin2x+2cos2x+2化为f(x)=2sin(2x+
sin2x+2cos2x+2化为f(x)=2sin(2x+ )+3即可求得f(x)最小正周期和值域;
)+3即可求得f(x)最小正周期和值域; )+3,可求得f(
)+3,可求得f( )=4;在△ABC中,利用面积公式S△=
)=4;在△ABC中,利用面积公式S△= bcsinA,c=1,可求得b=2,再由余弦定理可求得a.
bcsinA,c=1,可求得b=2,再由余弦定理可求得a.

科目:高中数学 来源:2010-2011学年浙江省杭州师大附中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
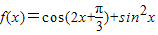 .
.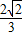 ,A为锐角,且
,A为锐角,且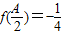 ,
,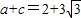 ,求△ABC的面积.
,求△ABC的面积.查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京四中高二(下)期中数学试卷(文科)(解析版) 题型:解答题
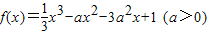 .
.查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省深圳市龙岗区高二(上)期末数学试卷(文科)(解析版) 题型:解答题
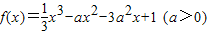 .
.查看答案和解析>>
科目:高中数学 来源:2007-2008学年北京市朝阳区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
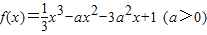 .
.查看答案和解析>>
科目:高中数学 来源:2007-2008学年北京市朝阳区高三(上)期末数学试卷(理科)(解析版) 题型:解答题
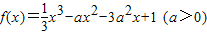 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com