
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
(1)求椭圆的标准方程;
(2)设圆C经过点F,且被直线l截得的弦长为4,求使OC长最小时圆C的方程.
 |
解:(1)设椭圆的标准方程为![]() +
+![]() =1(a>b>0).
=1(a>b>0).
由题意可得![]() ,………………………………………………………………………2分
,………………………………………………………………………2分
解得a=2![]() ,c=2.…………………………………………………………………………4分
,c=2.…………………………………………………………………………4分
从而b2=a2-c2=4.
所以椭圆的标准方程为![]() +
+![]() =1.……………………………………………………………6分
=1.……………………………………………………………6分
(2)设圆C的方程为(x-m)2+(y-n)2=r2,r>0.
由圆C经过点F(2,0),得(2-m)2+n2=r2, ①……………………………7分
由圆C被l截得的弦长为4,得|4-m|2+(![]() )2=r2, ②……………………………8分
)2=r2, ②……………………………8分
联立①②,消去r得:n2=16-4m.………………………………………………………10分
所以OC=![]() =
=![]() =
=![]() .……………………………………12分
.……………………………………12分
因为由n2≥0可得m≤4,
所以当m=2时,OC长有最小值2![]() .……………………………………………………14分
.……………………………………………………14分
此时n=±2![]() ,r=2
,r=2![]() ,故所求圆C的方程为(x-2)2+(y±2
,故所求圆C的方程为(x-2)2+(y±2![]() )2=8.………………16分
)2=8.………………16分


 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
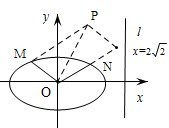 如图,椭圆的中心为原点O,离心率e=
如图,椭圆的中心为原点O,离心率e=
| ||
| 2 |
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
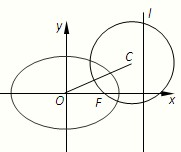 如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.查看答案和解析>>
科目:高中数学 来源: 题型:
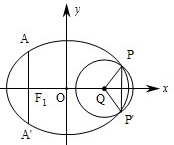
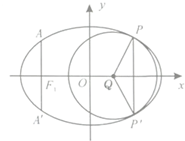 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率e=
| ||
| 2 |
查看答案和解析>>
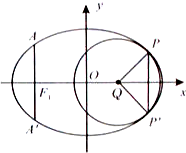
科目:高中数学 来源:2014届河南安阳一中高二第一次阶段测试数学试卷(奥数班)(解析版) 题型:解答题
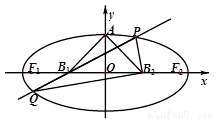
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左右焦点分别为 ,线段
,线段 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形.
是面积为4的直角三角形.
(Ⅰ)求该椭圆的离心率和标准方程;
(Ⅱ)过 做直线
做直线 交椭圆于P,Q两点,使
交椭圆于P,Q两点,使 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com