
【题目】如图,在四棱锥A-EFCB中,![]() 为等边三角形,平面AEF
为等边三角形,平面AEF![]() 平面EFCB,
平面EFCB,![]() ,
,![]() ,
,![]() ,
,![]() ,O为EF的中点.
,O为EF的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角F-AE-B的余弦值;
(Ⅲ)若BE![]() 平面AOC,求a的值.
平面AOC,求a的值.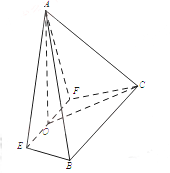
【答案】(I)证明见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】
(I)由于平面AEF![]() 平面EFCB,
平面EFCB,![]() 为等边三角形,O为EF的中点,则
为等边三角形,O为EF的中点,则![]() ,根据面面垂直性质定理,所以AO
,根据面面垂直性质定理,所以AO![]() 平面EFCB,又
平面EFCB,又![]() 平面EFCB,则
平面EFCB,则![]() .
.
(II) 取CB的中点D,链接OD,以O为原点,分别以OE,OD,OA为x,y,z轴建立空间直角坐标系,A![]() ,E
,E![]() ,B
,B![]() ,
,![]()
![]() ,
,![]() ,由于平面AEF与Y轴垂直,则设平面AEF的法向量为
,由于平面AEF与Y轴垂直,则设平面AEF的法向量为![]() ,设平面AEB的法向量
,设平面AEB的法向量![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,y=-1,则
,y=-1,则![]() ,二面角F-AE-B的余弦值cos(
,二面角F-AE-B的余弦值cos(![]() ,
,![]() )=
)=![]() =
=![]() ,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为
,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为![]() .
.
(Ⅲ)由(I)知![]() 平面EFCB,则
平面EFCB,则![]() ,若
,若![]() 平面
平面![]() ,只需
,只需![]() ,
,![]() ,又
,又![]() ,
,![]() ,解得
,解得![]() 或
或![]() ,由于
,由于![]() ,则
,则![]() .
.
【考点精析】利用向量语言表述线线的垂直、平行关系对题目进行判断即可得到答案,需要熟知设直线![]() 的方向向量分别是
的方向向量分别是![]() ,则要证明
,则要证明![]() ∥
∥![]() ,只需证明
,只需证明![]() ∥
∥![]() ,即
,即![]() ;则要证明
;则要证明![]() ,只需证明
,只需证明![]() ,即
,即![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】(2015·湖北)设![]() . 若p:
. 若p:![]() 成等比数列;
成等比数列;
q:![]() ,则( )
,则( )
A.p是q的充分条件,但不是q的必要条件
B.p是q的必要条件,但不是q的充分条件
C.p是q的充分必要条件
D.p既不是q的充分条件,也不是q的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)一种画椭圆的工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆ON可绕O转动,长杆MN通过N处铰链
的中点,短杆ON可绕O转动,长杆MN通过N处铰链
与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕![]() 转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为
转动,M处的笔尖画出的椭圆记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)(Ⅰ)求椭圆C的方程;
(2)(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.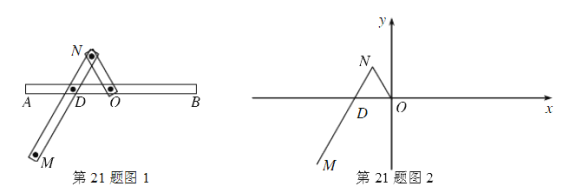
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示,若将运动员按成绩由好到差编为![]() 号,再用系统抽样方法从中抽取7人,则其中成绩在区间
号,再用系统抽样方法从中抽取7人,则其中成绩在区间![]() 上的运动员人数是
上的运动员人数是 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求 ![]() 的值;
的值;
(3)在满足(2)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点值代替,记 ![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程![]() 的有一个正实根,一个负实根,
的有一个正实根,一个负实根,![]() ;
;
③![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]()
④函数![]() 的值域是
的值域是![]() .
.
其中正确命题的序号是_____(把所有正确命题的序号都写上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com