
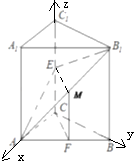
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.
(1)当E是棱CC1的中点时,求证:CF∥平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A﹣EB1﹣B的大小是45°?若存在,求出CE的长,若不存在,请说明理由.
【答案】
(1)解:取AB1中点M,连接EM、FM
∵△AB1B中,M、F分别是AB、AB1的中点,
∴MF∥B1B且MF= ![]() B1B,
B1B,
又∵矩形BB1C1C中,CE∥B1B且CE= ![]() B1B,
B1B,
∴MF∥CE且MF=CE,可得四边形MFCE是平行四边形
∴CF∥EM
∵CF平面EAB1,EM平面EAB1,
∴CF∥平面AEB1
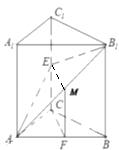
(2)解:以CA、CB、CC1为x、y、z轴,建立如图空间直角坐标系,
可得A(2,0,0),B1(0,2,4),设CE=m,得E(0,0,m)
∴ ![]() =(﹣2,0,m),
=(﹣2,0,m), ![]() =(﹣2,2,4)
=(﹣2,2,4)
设平面AEB1的法向量为 ![]() =(x,y,z)
=(x,y,z)
则有 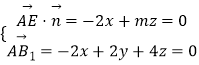 ,解之并取z=2,得
,解之并取z=2,得 ![]() =(m,m﹣4,2)
=(m,m﹣4,2)
∵平面EB1B的法向量为 ![]() =(2,0,0),
=(2,0,0),
∴当二面角A﹣EB1﹣B的大小是45°时,有
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,解之得m=
,解之得m= ![]() .
.
因此,在棱CC1上存在点E,当CE= ![]() 时,二面角A﹣EB1﹣B的大小是45°.
时,二面角A﹣EB1﹣B的大小是45°.
【解析】(1)根据题意作出辅助线,由已知条件可得线线平行进而得出直线与平面平行。(2)根据题意建立空间直角坐标系,分别求出各个点以及向量的坐标,设出平面AEB1的法向量再根据法向量和向量AE的数量积等于零求出法向量的坐标,再根据数量积的运算公式结合二面角A﹣EB1﹣B的大小求出余弦值进而得到m的值,即可得证点E的存在。
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
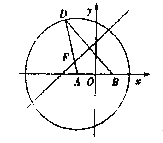
【题目】如图,在平面直角坐标系![]() 中,圆
中,圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,线段
上的动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设
,设![]() 分别为点
分别为点![]() 的横坐标,定义函数
的横坐标,定义函数![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 是偶函数;③
是偶函数;③![]() 在定义域上是增函数;
在定义域上是增函数;
④![]() 图象的两个端点关于圆心
图象的两个端点关于圆心![]() 对称;
对称;
⑤动点![]() 到两定点
到两定点![]() 的距离和是定值.
的距离和是定值.
其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点.
的中点.
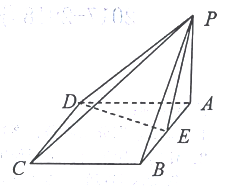
(1)求证:平面![]() 平面
平面![]() ;
;
(2)棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定
?若存在,确定![]() 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设你家订了一份报纸,送报人可能在早上6点—8点之间把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间.
问:离家前不能看到报纸(称事件![]() )的概率是多少?(须有过程)
)的概率是多少?(须有过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com