
【题目】已知椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 原点到过A(a,0),B(0,﹣b)两点的直线的距离是
, 原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
(1)求椭圆的方程;
(2)已知直线y=kx+1(k≠0)交椭圆于不同的两点E,F,且E,F都在以B为圆心的圆上,求k的取值范围.
【答案】解:(1)直线AB的方程为:bx﹣ay﹣ab=0
∵原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
∴![]() =
=![]()
∴![]() ①
①
∵椭圆![]()
![]() 的离心率e=
的离心率e=![]() ,
,
∴![]()
∴a2=4b2②
②代入①,可得b2=4,
∴a2=16
∴椭圆的方程为![]() ;
;
(2)由题意,B(0,﹣2)
设E(x1 , y1),F(x2 , y2),由E,F在圆上,得x12+(y1+2)2=x22+(y2+2)2…③,
由E,F在直线y=kx+1得y1=kx1+1,y2=kx2+1,
代入③式,可得(1+k2)(x1+x2)(x1﹣x2)+6k(x1﹣x2)=0,
因为E,F为直线上不同两点,所以x1≠x2 , 所以(1+k2)(x1+x2)+6k=0,
即x1+x2=-![]() ④
④
又由E,F在椭圆上,将y=kx+1代入![]() ,得(1+4k2)x2+8kx﹣12=0,
,得(1+4k2)x2+8kx﹣12=0,
由根与系数的关系,x1+x2=-![]() …⑤,
…⑤,
将④⑤两式联立求解得k=0(舍)或k=±![]() ,
,
故k═±![]() .
.
【解析】(1)直线AB的方程为:bx﹣ay﹣ab=0,利用原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() , 可得
, 可得![]() =
=![]() , 利用椭圆
, 利用椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 可得
, 可得![]() , 从而可求b2=4,
, 从而可求b2=4,
a2=16,故可求椭圆的方程;
(2)由题意,B(0,﹣2),设E(x1 , y1),F(x2 , y2),由E,F在圆上,得x12+(y1+2)2=x22+(y2+2)2 , 由E,F在直线y=kx+1得y1=kx1+1,y2=kx2+1,代入可得(1+k2)(x1+x2)(x1﹣x2)+6k(x1﹣x2)=0,从而可得x1+x2=-![]() ;将y=kx+1代入
;将y=kx+1代入![]() , 得(1+4k2)x2+8kx﹣12=0,由根与系数的关系,可得x1+x2=-
, 得(1+4k2)x2+8kx﹣12=0,由根与系数的关系,可得x1+x2=-![]() , 从而可求得k的值.
, 从而可求得k的值.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() ,(θ为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρ=
,(θ为参数),以坐标原点为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρ= ![]() sinθ+cosθ,曲线C3的极坐标方程是θ=
sinθ+cosθ,曲线C3的极坐标方程是θ= ![]() . (Ⅰ)求曲线C1的极坐标方程;
. (Ⅰ)求曲线C1的极坐标方程;
(Ⅱ)曲线C3与曲线C1交于点O,A,曲线C3与曲线C2曲线交于点O,B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以坐标原点
为极点,以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 上的点到直线
上的点到直线![]() 的最大距离为6,求实数
的最大距离为6,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD=2,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD;
(3)若PC⊥CD,PB=4,求四棱锥P﹣ABCD的体积.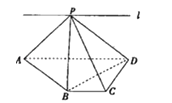
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角![]() 为的扇形
为的扇形![]() ,小区的两个出入口设置在点
,小区的两个出入口设置在点![]() 及点
及点![]() 处,且小区里有一条平行于
处,且小区里有一条平行于![]() 的小路
的小路![]() 。
。

(1)已知某人从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,从
分钟,从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,若此人步行的速度为每分钟
分钟,若此人步行的速度为每分钟![]() 米,求该扇形的半径
米,求该扇形的半径![]() 的长(精确到
的长(精确到![]() 米)
米)
(2)若该扇形的半径为![]() ,已知某老人散步,从
,已知某老人散步,从![]() 沿
沿![]() 走到
走到![]() ,再从
,再从![]() 沿
沿![]() 走到
走到![]() ,试确定
,试确定![]() 的位置,使老人散步路线最长。
的位置,使老人散步路线最长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com