
【题目】已知斜三棱柱![]() 的棱长都是
的棱长都是![]() ,侧棱与底面成60°角,侧面
,侧棱与底面成60°角,侧面![]() 底面
底面![]() .
.

(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
【答案】(1)证明见解析(2)45°
【解析】
(1)根据题意,作![]() 于点
于点![]() ,连接
,连接![]() ,由平面
,由平面![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 是侧棱与底面所成的角,又因为点
是侧棱与底面所成的角,又因为点![]() 为
为![]() 的中点.,
的中点.,![]() 是正三角形,所以
是正三角形,所以![]() .,再由线面垂直的判定定理,得到
.,再由线面垂直的判定定理,得到![]() 平面
平面![]() ,从而证得
,从而证得![]() ..
..
(2)由![]() 是平面
是平面![]() 与平面
与平面![]() 的一个交点,根据平面的基本性质,平面
的一个交点,根据平面的基本性质,平面![]() 与平面
与平面![]() 有且仅有一条过点
有且仅有一条过点![]() 的交线,设为
的交线,设为![]() ,根据面面平行的性质定理,得
,根据面面平行的性质定理,得 ![]() ,
,![]() ,再由(1)知
,再由(1)知![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 为所求锐二面角的平面角,然后再求解..
为所求锐二面角的平面角,然后再求解..
(1)如图,作![]() 于点
于点![]() ,连接
,连接![]() .
.
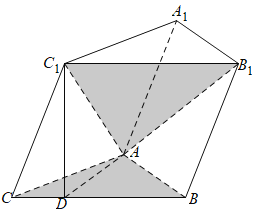
∵平面![]() 底面
底面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 为
为![]() 在底面
在底面![]() 上的射影,
上的射影,
![]() ,
,![]() ,
,
∴点![]() 为
为![]() 的中点.
的中点.
![]() 是正三角形,
是正三角形,
![]() .
.
![]() ,
,
![]() 平面
平面![]() ,
,
![]() .
.
(2)![]() 是平面
是平面![]() 与平面
与平面![]() 的一个交点,
的一个交点,
∴平面![]() 与平面
与平面![]() 有且仅有一条过点
有且仅有一条过点![]() 的交线,设为
的交线,设为![]() ,如图.
,如图.
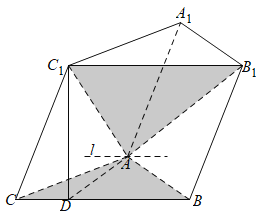
∵平面![]() 平面
平面![]() ,
,
∴由两平面平行的性质,知![]() ,又
,又![]() ,
,
由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() 为所求锐二面角的平面角,
为所求锐二面角的平面角,
![]() .
.
故平面![]() 与平面
与平面![]() 所成的锐二面角为45°.
所成的锐二面角为45°.


科目:高中数学 来源: 题型:
【题目】如图,E,F分别为边长为2的正方形ABCD的边BC,CD的中点,沿图中虚线折起,使得B,C,D三点重合于点O,点O在平面AEF上的射影H.
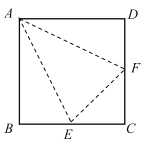
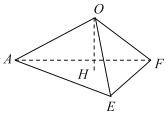
(1)求证:面![]() 面OEA;
面OEA;
(2)求证:点H是![]() 的垂心;
的垂心;
(3)求OH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由![]() 开始依次按如下规则将某些数染成蓝色:先染
开始依次按如下规则将某些数染成蓝色:先染![]() ;再染两个偶数
;再染两个偶数![]() ;再染
;再染![]() 后面的最临近的
后面的最临近的![]() 个连续奇数
个连续奇数![]() ;再染
;再染![]() 后面的最临近的
后面的最临近的![]() 个连续偶数
个连续偶数![]() ;再染此后最临近的
;再染此后最临近的![]() 个连续奇数
个连续奇数![]() .按此规则一直染下去,得到一蓝色子数列
.按此规则一直染下去,得到一蓝色子数列![]()
![]() ,则在这个蓝色子数列中,由
,则在这个蓝色子数列中,由![]() 开始的第
开始的第![]() 个数是________.
个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
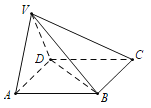
(Ⅰ)证明AB⊥平面VAD;
(Ⅱ)求面VAD与面VDB所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,四边形
,四边形![]() 满足
满足![]() ,
,![]() 为侧棱
为侧棱![]() 上的任意一点.
上的任意一点.

(1)求证:平面![]() 平面
平面![]() .
.
(2)是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直?若存在,写出证明过程并求出线段
垂直?若存在,写出证明过程并求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个点A(2,1),B(3,2),D(-1,4).
(1)求证:![]() ⊥
⊥![]() ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD两对角线所夹锐角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)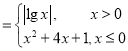 ,g(x)=f(x)-a,
,g(x)=f(x)-a,
(1)讨论函数g(x)的零点个数,并写出相应的实数a的取值范围;
(2)当函数g(x)有四个零点分别为x1,x2,x3,x4时,求x1+x2+x3+x4的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com